
分析 (1)、根据题意,结合二次函数的性质分析可得$\left\{\begin{array}{l}{△=(k-2)^{2}-4({k}^{2}+3k+5)>0}\\{f(-2)=4+2(k-2)+({k}^{2}+3k+5)>0}\\{\frac{k-2}{2}<-2}\end{array}\right.$,解可得k的范围,即可得答案;
(2)若函数的两个零点是α和β,即方程x2-(k-2)x+k2+3k+5=0的两根为α和β,首先方程有2根,则有△=(k-2)2-4(k2+3k+5)≥0,解可得k的范围,进而由根与系数的关系的关系可得$\left\{\begin{array}{l}{α+β=k-2}\\{α•β={k}^{2}+3k+5}\end{array}\right.$,分析有α2+β2=(α+β)-2αβ=-k2-10k-6,结合k的范围,分析可得(-k2-10k-6)的范围,即可得答案.
解答 解:(1)根据题意,函数f(x)=x2-(k-2)x+k2+3k+5有两个大于-2的零点,
则二次函数f(x)=x2-(k-2)x+k2+3k+5与x轴有2个交点,且交点都在(-2,0)的右侧,
则有$\left\{\begin{array}{l}{△=(k-2)^{2}-4({k}^{2}+3k+5)>0}\\{f(-2)=4+2(k-2)+({k}^{2}+3k+5)>0}\\{\frac{k-2}{2}<-2}\end{array}\right.$,
解可得$\frac{-5+\sqrt{5}}{2}$<k<-$\frac{4}{3}$,
故k的取值范围是($\frac{-5+\sqrt{5}}{2}$,-$\frac{4}{3}$);
(2)若函数的两个零点是α和β,即方程x2-(k-2)x+k2+3k+5=0的两根为α和β,
则必有△=(k-2)2-4(k2+3k+5)≥0,
解可得-4≤k≤-$\frac{4}{3}$,
又由$\left\{\begin{array}{l}{α+β=k-2}\\{α•β={k}^{2}+3k+5}\end{array}\right.$,
α2+β2=(α+β)2-2αβ=-k2-10k-6,
又由-4≤k≤-$\frac{4}{3}$,
令t=-k2-10k-6,则t=-(k+5)2+19,
又由-4≤k≤-$\frac{4}{3}$,
则$\frac{50}{9}$≤t≤18;
则α2+β2的取值范围是[$\frac{50}{9}$,18]
点评 本题考查二次函数的性质,涉及函数零点的定义与判定,关键是正确掌握理解函数与方程的关系.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [60,70) | ③ | 0.16 |
| [70,80) | 14 | ② |
| [80,90) | 16 | 0.32 |
| [90,100] | ① | 0.24 |
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
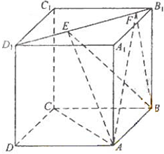 如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=$\frac{1}{2}$,给出下列命题:
如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=$\frac{1}{2}$,给出下列命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | (4,+∞) | C. | (-∞,-3)∪(4,+∞) | D. | (-∞,-3)∪($\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com