
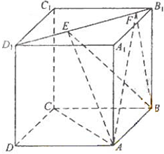
 如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=$\frac{1}{2}$,给出下列命题:
如图,正方体ABCD-A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF=$\frac{1}{2}$,给出下列命题:分析 通过证明线面垂直,可证AC⊥BE,故①正确;
根据线面平行的判断定理,可证EF∥平面ABCD,故②正确;
△BEF与△AEF底都是EF,但高不相等,所以面积不相等,故③错误;
根据三棱锥的底面面积与EF的位置无关,高也与EF的位置无关,所以体积为定值,故④正确;
例举两个特殊位置的异面直线所成的角的大小,根据大小不同可知⑤错误.
解答 解:对于①:∵AC⊥BD,AC⊥DD1,BD∩DD1=D,∴AC⊥面BB1D1D,∵BE?面BB1D1D,∴AC⊥BE,故①正确;
对于②:∵EF∥BD,BD?平面ABCD,EF?平面ABCD,∴EF∥平面ABCD,故②正确;
对于③:连结A1C1,交B1D1于点O1,连结AO1,则AO1⊥EF,∵${S}_{△AEF}=\frac{1}{2}EF•A{O}_{1}$,${S}_{△BEF}=\frac{1}{2}EF•B{B}_{1}$,且AO1≠BB1,∴△AEF的面积与△BEF的面积不相等,故③错误;
对于④:连结BD,交AC于点O,∵AC⊥面BB1D1D,∴AO⊥面BEF,即AO是三棱锥A-BEF的高,∴${V}_{A-BEF}=\frac{1}{3}AO•{S}_{△BEF}$=$\frac{1}{3}×\frac{\sqrt{2}}{2}×\frac{1}{2}×\frac{1}{2}×1$=$\frac{\sqrt{2}}{24}$,故④正确;
对于⑤:设异面直线所成的角为α,当E与D1重合时,sinα=$\frac{1}{2}$,α=30°;当F与B1重合时tanα=$\frac{\sqrt{2}}{2}$,所以异面直线AE、BF所成的角不是定值,故⑤错误.
故答案为:①②④
点评 本题考查了异面直线所成的角及求法,考查了线面垂直、面面平行的性质,考查了学生的空间想象能力及作图分析能力.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 半径为3的圆面积 | B. | 半径为3的半圆面积 | ||
| C. | 半径为3的圆面积的四分之一 | D. | 半径为3的半圆面积的四分之一 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com