练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．下列函数中，在（0，+∞）上单调递增的函数是（　　）
    A．f（x）=$\frac{1}{x}$B．f（x）=sinxC．f（x）=cosxD．f（x）=x${\;}^{\frac{1}{2}}$

    分析 根据反比例函数和正余弦函数的单调性便可判断前三项错误，而根据增函数的定义和f（x）=${x}^{\frac{1}{2}}$的图象便可判断选项D正确．

    解答 解：A.$f（x）=\frac{1}{x}$在（0，+∞）上单调递减，∴该选项错误；
    B．f（x）=sinx在（0，+∞）上没有单调性，∴该选项错误；
    C．f（x）=cosx在（0，+∞）上没有单调性，∴该选项错误；
    D.$f（x）={x}^{\frac{1}{2}}$在（0，+∞）上单调递增，∴该选项正确．
    故选：D．

    点评 考查反比例函数的单调性，正弦函数和余弦函数的单调性，以及单调性的定义，要清楚$f（x）={x}^{\frac{1}{2}}$的图象．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届浙江嘉兴市高三上学期基础测试数学试卷（解析版） 题型：填空题

    在的展开式中，含项的二项式系数为 ；系数为 ．（均用数字作答）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知集合A={x|2x＞8}，B={x|x2-3x-4＜0}．
    （1）求A，B；
    （2）设全集U=R，求（∁UA）∩B．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．在等腰三角形ABC中，过直角顶点C在∠ACB内作一条射线CD与线段AB交于点D，则AD＜AC的概率是（　　）
    A．$\frac{{\sqrt{2}}}{2}$B．$\frac{1}{4}$C．$\frac{{2-\sqrt{2}}}{2}$D．$\frac{3}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．函数f（x）=lgx-sinx在（0，+∞）的零点个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．在（x-$\frac{1}{\sqrt{2}x}$）9的展开式中，x5的系数为18．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．计算：$\frac{tan（π-α）sin（-α+\frac{3π}{2}）}{sin（-π-α）}$+sin$\frac{11π}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

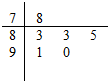    7．对某同学的6次数学测试成绩（满分100分）进行统计，作出的茎叶如图所示，给出关于该同学数学成绩的以下说法：
    ①中位数为83；②众数为83；③平均数为85；④极差为12．
    其中正确说法序号是（　　）
    A．①②B．③④C．②③D．①③

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知离心率为e的椭圆Γ：$\frac{{x}^{2}}{{a}^{2}-4}$+$\frac{{y}^{2}}{{a}^{2}}$=1（a＞2）的上、下焦点分别为F1和F2，过点（0，2）且不与y轴垂直的直线与椭圆交于M，N两点，若△MNF2为等腰直角三角形，则e=（　　）
    A．$\sqrt{3}$-$\sqrt{2}$B．$\frac{\sqrt{3}}{2}$C．$\sqrt{6}$$-\sqrt{3}$D．$\frac{\sqrt{6}}{3}$

    查看答案和解析>>

    同步练习册答案