
分析 利用两角和与差的三角函数化简求解即可.
解答 解:tan($\frac{π}{4}$-x)=$\frac{5}{13}$,可得$\frac{1-tanx}{1+tanx}=\frac{5}{13}$,$\frac{cosx-sinx}{cosx+sinx}$=$\frac{5}{13}$,解得tanx=$\frac{4}{9}$.
$\frac{co{s}^{2}x-si{n}^{2}x}{\frac{\sqrt{2}}{2}(cosx-sinx)}$=$\sqrt{2}$(cosx+sinx)=$±\sqrt{2}$×$\sqrt{\frac{({sinx+cosx)}^{2}}{si{n}^{2}x+co{s}^{2}x}}$=$±\sqrt{2}×$$\sqrt{\frac{ta{n}^{2}x+2tanx+1}{ta{n}^{2}x+1}}$=$±\sqrt{2}×\sqrt{\frac{\frac{16}{81}+\frac{8}{9}+1}{\frac{16}{81}+1}}$
=$±\frac{13\sqrt{194}}{97}$.
点评 本题考查两角和与差的三角函数,考查计算能力.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
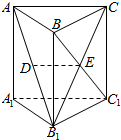 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,BC1∩B1C=E.求证:
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,BC1∩B1C=E.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
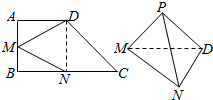 在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.
在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$),k∈Z | B. | (kπ,(k+1)π),k∈Z | ||
| C. | (kπ-$\frac{3π}{4}$,kπ+$\frac{π}{4}$),k∈Z | D. | (kπ-$\frac{π}{4}$,kπ+$\frac{3π}{4}$),k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/份 | 440 | 400 | 360 | 320 | 280 | 240 | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com