
分析 (1)由解析式令log2x=t即x=2t,代入解析式化简求出f(t),将t化为x可得f(x)的解析式;
(2)由(1)化简f(x)=(a-1)•4x,根据指数函数的性质分类讨论,分别由指对互化的式子求出x的表达式.
解答 解:(1)令log2x=t即x=2t,则f(t)=a•(2t)2-2•2t+1-a
即f(x)=a•22x-2•2x+1-a,x∈R
(2)由f(x)=(a-1)•4x得:a•22x-2•2x+1-a=(a-1)•4x,
化简得,22x-2•2x+1-a=0,即(2x-1)2=a,
当a<0时,方程无解;
当a≥0时,解得${2^x}=1±\sqrt{a}$,
所以若0≤a<1,则$x={log_2}(1±\sqrt{a})$,
若a≥1,则$x={log_2}(1+\sqrt{a})$.
点评 本题考查利用换元法求函数的解析式,指对互化、指数函数的性质的应用,考查分类讨论思想,属于中档题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:选择题
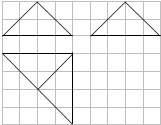
| A. | 8+12$\sqrt{2}$ | B. | 16+24$\sqrt{2}$ | C. | $\frac{1}{3}(8+12\sqrt{2})$ | D. | 4+6$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
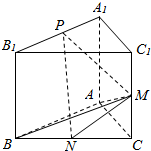 如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.
如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 83 | B. | $\sqrt{83}$ | C. | 98$+56\sqrt{2}$ | D. | $\sqrt{98+56\sqrt{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com