
已知函数f(x)=4x+m·2x+1有且仅有一个零点,求m的取值范围,并求出该零点.
科目:高中数学 来源: 题型:
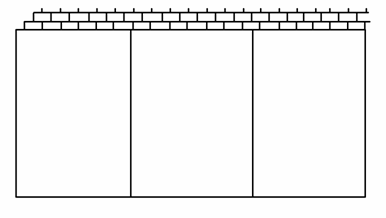
有一批材料可以建成200m长的围墙,如果用此批材料在一边靠墙的地方围成一块矩形场地,中间用同样材料隔成三个面积相等的矩形(如图所示),则围成场地的最大面积为________(围墙的厚度不计).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=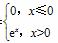 ,则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是( )
,则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是( )
A.[0,1) B.(-∞,1)
C.(-∞,1]∪(2,+∞) D.(-∞,0]∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
某航空公司经营A、B、C、D这四个城市之间的客运业务.它的部分机票价格如下:A—B为2000元;A—C为1600元;A—D为2500元;B—C为1200元;C—D为900元.若这家公司规定的机票价格与往返城市间的直线距离成正比,则B—D的机票价格为( )
(注:计算时视A、B、C、D四城市位于同一平面内)
A.1000元 B.1200元
C.1400元 D.1500元
查看答案和解析>>
科目:高中数学 来源: 题型:
已知两定点A(-2,0),B(1,0),如果动点P满足|PA|=2|PB|,则点P的轨迹所包围的图形的面积等于( )
A.π B.4π
C.8π D.9π
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C:x2+y2-2x+4y-4=0,是否存在斜率为1的直线l,使以l被圆截得的弦AB为直径的圆过原点?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com