
分析 先设出侧棱长为l,正三棱锥的底边长为a,利用异面直线所成角的概念及已知SD与BC所成角的余弦值为$\frac{{\sqrt{3}}}{6}$,建立l和a的方程,得出正三棱锥S-ABC为正四面体,棱长为4,外接球的半径,即可得出结论.
解答 解:由题意画出图形:由于三棱锥S-ABC为正三棱锥
设侧棱为l,底面边长为a,因为D是AB的中点,且SD与BC所成角的余弦值为$\frac{{\sqrt{3}}}{6}$,
取AC的中点E,因为DE∥BC,所以cos∠SDE=$\frac{\sqrt{3}}{6}$,
所以$\frac{\frac{a}{4}}{\sqrt{{l}^{2}-\frac{{a}^{2}}{4}}}$=$\frac{\sqrt{3}}{6}$,所以a=l,
所以正三棱锥S-ABC为正四面体,棱长为4,外接球的半径为$\frac{3}{4}×\sqrt{16-\frac{16}{3}}$=$\sqrt{6}$,
∴三棱锥S-ABC外接圆的表面积为4π•6=24π,
故答案为24π.
点评 本题重点考查了异面直线所成角的概念,还考查了直线与平面所成的线面角的概念及解题过程中方程的解题思想,属于中档题,解题的关键就是寻找线面所成角.


科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | $\frac{3\sqrt{7}}{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | $\frac{{3\sqrt{15}}}{2}$ | C. | $-\frac{{4\sqrt{5}}}{5}$ | D. | $-\frac{{3\sqrt{15}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
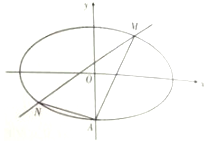 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点$(\sqrt{2},0)$,且焦距为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点$(\sqrt{2},0)$,且焦距为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com