
【题目】已知函数![]() 的图象与
的图象与![]() 轴的交点至少有一个在原点右侧.
轴的交点至少有一个在原点右侧.
(1)求实数![]() 的取值范围;
的取值范围;
(2)令![]() ,求
,求![]() 的值(其中
的值(其中![]() 表示不超过
表示不超过![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() );
);
(3)对(2)中的![]() 求函数
求函数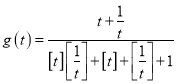 的值域.
的值域.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)分![]() 和
和![]() 两种情况讨论,在
两种情况讨论,在![]() 时进行验证即可,在
时进行验证即可,在![]() 时,由
时,由![]() 可分二次函数
可分二次函数![]() 有且只有一个零点且为正零点、一个正零点和一个负零点、两个正零点三种情况进行分类讨论,由此可得出实数
有且只有一个零点且为正零点、一个正零点和一个负零点、两个正零点三种情况进行分类讨论,由此可得出实数![]() 的取值范围;
的取值范围;
(2)求出![]() ,可得出
,可得出![]() ,然后分
,然后分![]() 和
和![]() 两种情况讨论,根据定义得出
两种情况讨论,根据定义得出![]() 的值;
的值;
(3)分![]() 、
、![]() 、
、![]() 三种情况讨论,在
三种情况讨论,在![]() 时代入函数
时代入函数![]() 的解析式计算即可,在
的解析式计算即可,在![]() 时,利用函数
时,利用函数![]() 的单调性得出该函数的值域,在
的单调性得出该函数的值域,在![]() 时,考查
时,考查![]() ,结合函数的单调性来得出值域,由此可得出函数
,结合函数的单调性来得出值域,由此可得出函数![]() 的值域.
的值域.
(1)①若![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,此时,函数
,此时,函数![]() 只有一个正零点,合乎题意;
只有一个正零点,合乎题意;
②若![]() ,由于
,由于![]() .
.
(i)若函数![]() 有且只有一个零点且为正数,则
有且只有一个零点且为正数,则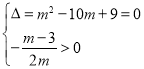 ,解得
,解得![]() ;
;
(ii)若函数![]() 有一个正零点和一个负零点,则
有一个正零点和一个负零点,则![]() ,解得
,解得![]() ;
;
(iii)若函数![]() 有两个正零点时,则
有两个正零点时,则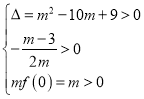 ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)![]() ,
,![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() ;当
;当![]() 时,
时,![]() ,此时
,此时![]() .
.
因此,![]() ;
;
(3)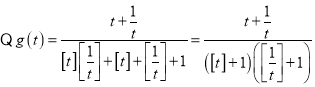 .
.
①当![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ,
,![]() ,则
,则![]() 单调递增,此时
单调递增,此时![]() ;
;
③当![]() 时,设
时,设![]() ,则
,则![]() ,
,![]() ,
,
此时,![]() 在
在![]() 上单调递增,则
上单调递增,则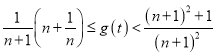 .
.
设![]() ,
,
则![]()
![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 且
且![]() 时,
时,![]() ,数列
,数列![]() 单调递增,
单调递增,![]() ;
;
设![]() ,当
,当![]() 且
且![]() ,数列
,数列![]() 单调递增,
单调递增,
当![]() 时,
时,![]() .
.
所以,当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() .
.
综上所述,函数![]() 的值域为
的值域为![]() .
.


科目:高中数学 来源: 题型:
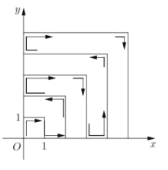
【题目】如图,一个粒子从原点出发,在第一象限和两坐标轴正半轴上运动,在第一秒时它从原点运动到点![]() ,接着它按图所示在
,接着它按图所示在![]() 轴、
轴、![]() 轴的垂直方向上来回运动,且每秒移动一个单位长度,那么,在2018秒时,这个粒子所处的位置在点______.
轴的垂直方向上来回运动,且每秒移动一个单位长度,那么,在2018秒时,这个粒子所处的位置在点______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已定义![]() ,已知函数
,已知函数![]() 的定义域都是
的定义域都是![]() ,则下列四个命题中为真命题的是_________.(写出所有真命题的序号)
,则下列四个命题中为真命题的是_________.(写出所有真命题的序号)
① 若![]() 都是奇函数,则函数
都是奇函数,则函数![]() 为奇函数.
为奇函数.
② 若![]() 都是偶函数,则函数
都是偶函数,则函数![]() 为偶函数.
为偶函数.
③ 若![]() 都是增函数,则函数
都是增函数,则函数![]() 为增函数.
为增函数.
④ 若![]() 都是减函数,则函数
都是减函数,则函数![]() 为减函数.
为减函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自湖北爆发新型冠状病毒肺炎疫情以来,湖北某市医护人员和医疗、生活物资严重匮乏,全国各地纷纷驰援.某运输队接到从武汉送往该市物资的任务,该运输队有8辆载重为6t的A型卡车,6辆载重为10t的B型卡车,10名驾驶员,要求此运输队每天至少运送240t物资.已知每辆卡车每天往返的次数为A型卡车5次,B型卡车4次,每辆卡车每天往返的成本A型卡车1200元,B型卡车1800元,则每天派出运输队所花的成本最低为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com