
分析 (1)求出a,b的值,通过讨论c的范围,解不等式即可;
(2)不等式对任意m恒成立,可把m看作变量,x为常数,构造一次函数f(m),根据其单调性得到不等式组,再解出即可.
解答 解(1)∵函数f(x)=ax2-3x+b,若f(x)>0的解集为{x|x<1或x>2}.
∴1,2是方程ax2-3x+b=0的根,
∴$\left\{\begin{array}{l}{a-3+b=0}\\{4a-6+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$.
∴不等式$\frac{x-c}{ax-b}$>0(c为常数),即$\frac{x-c}{x-2}$>0,
c>2时,解得:x>c或x<2,
c<2时,解得:x>2或x<c,
故c>2时,不等式的解集是{x|x>c或x<2},
c<2时,不等式的解集是{x|x>2或x<c};
(2)若bx-1>m(ax2-1)在m∈[-2,2]上恒成立,
由(1)得:即2x-1>m(x2-1)在m∈[-2,2]上恒成立,
不等式2x-1>m(x2-1)可化为
m(x2-1)-2x+1<0…①
当x=1时,①式即-1<0,显然成立,
当x=-1时,①式即3<0,显然不成立,
当x≠±1时,令f(m)=m(x2-1)-2x+1,
由一次函数性质知,
不等式2x-1>m(x2-1)对任意m∈[-2,2]恒成立等价于,
$\left\{\begin{array}{l}{f(-2)<0}\\{f(2)<0}\end{array}\right.$,即 $\left\{\begin{array}{l}{-{2x}^{2}-2x+3<0}\\{{2x}^{2}-2x-1<0}\end{array}\right.$,
解得,($\frac{\sqrt{7}-1}{2}$,$\frac{\sqrt{3}+1}{2}$),
∴x∈($\frac{\sqrt{7}-1}{2}$,$\frac{\sqrt{3}+1}{2}$),
故答案为:($\frac{\sqrt{7}-1}{2}$,$\frac{\sqrt{3}+1}{2}$).
点评 本题主要考查不等式问题,考查转化思想,即确定主元,同时考查构造函数思想,应用函数的性质解决,解题时还应对参数进行讨论,是一道很好的题目,属于中档题.


科目:高中数学 来源: 题型:解答题
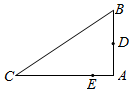 如图所示,D、E分别是△ABC的边AB、AC上的点(D、E不与边的端点重合).已知线段AD、AB的长分别为m、n,AE、AC的长是关于x的方程x2-18x+mn=0的两个根.
如图所示,D、E分别是△ABC的边AB、AC上的点(D、E不与边的端点重合).已知线段AD、AB的长分别为m、n,AE、AC的长是关于x的方程x2-18x+mn=0的两个根.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com