
分析 (Ⅰ)求得f(x)的导数,单调区间,可得f(x)的最大值为f(1);
(Ⅱ)由题意可得$m{x_2}^2+{x_2}ln{x_2}>m{x_1}^2+{x_1}ln{x_1}$恒成立,设φ(x)=mx2+xlnx,又0<x2<x1,则只需ϕ(x)在(0,+∞)上单调递减,求得导数,令导数小于等于0恒成立,运用参数分离和构造函数法,求出导数和单调区间,可得最值,即可得到所求m的范围;
(Ⅲ)结论:$2{e^{S_n}}$>2n+1.运用构造数列法和等比数列的通项公式,可得an=$\frac{{{2^{n-1}}}}{{1+{2^{n-1}}}}$.运用对数的运算性质和放缩法,结合裂项相消求和,即可得证.
解答 解:(Ⅰ)由题意得:$f'(x)=\frac{1}{x}-1=\frac{1-x}{x}$.
当x∈(0,1)时,f'(x)>0,当x∈(1,+∞)时,f'(x)<0,
因此,f(x)在(0,1)上单调递增,在(1,+∝)上单调递减.
所以f(x)max=f(1)=0,即函数f(x)的最大值为0;
(Ⅱ)若$m{x_2}^2-m{x_1}^2-{x_1}ln{x_1}+{x_2}ln{x_2}>0$恒成立,
则$m{x_2}^2+{x_2}ln{x_2}>m{x_1}^2+{x_1}ln{x_1}$恒成立,
设φ(x)=mx2+xlnx,又0<x2<x1,
则只需ϕ(x)在(0,+∞)上单调递减,
故ϕ′(x)=2mx+1+lnx≤0在(0,+∞)上成立,得:2m≤$-\frac{1+lnx}{x}$,
记t(x)=$-\frac{1+lnx}{x}$,则${t^'}(x)=\frac{lnx}{x^2}$,
于是可知t(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
故[t(x)]min=t(1)=-1,
因此存在m≤$-\frac{1}{2}$,使$m{x_2}^2-m{x_1}^2-{x_1}ln{x_1}+{x_2}ln{x_2}>0$恒成立;
(Ⅲ)由$\frac{1}{{{a_{n+1}}}}$=$\frac{{(1+{a_n}){a_n}}}{2a_n^2}$=$\frac{1}{2}$•$\frac{1}{a_n}$+$\frac{1}{2}$得:$\frac{1}{{{a_{n+1}}}}-1$=$\frac{1}{2}$$({\frac{1}{a_n}-1})$,又${a_1}=\frac{1}{2}$,
知,$\frac{1}{{{a_{n+1}}}}-1$=${({\frac{1}{2}})^n}$,即有an=$\frac{{{2^{n-1}}}}{{1+{2^{n-1}}}}$.
结论:$2{e^{S_n}}$>2n+1.
证明如下:
因为an∈(0,1),由(1)知x>0时x-1>lnx,则x>-1时x>ln(x+1).
所以an>ln(an+1)=$ln\frac{{{2^n}+1}}{{{2^{n-1}}+1}}$=ln(2n+1)-ln(2n-1+1)
故Sn=a1+a2+…+an
>[ln(21+1)-ln(20+1)]+[ln(22+1)-ln(21+1)]…[ln(2n+1)-ln(2n-1+1)]
=ln(2n+1)-ln(20+1)=$ln(\frac{{{2^n}+1}}{2})$,
即$2{e^{S_n}}$>2n+1.
点评 本题考查导数的运用:求单调区间和最值,考查不等式恒成立问题的解法,注意运用参数分离和函数的单调性,同时考查两式的大小比较,注意运用等比数列的通项公式和裂项相消求和,考查化简整理的运算能力,属于难题.


科目:高中数学 来源: 题型:填空题
 如图,直角坐标系x′Oy所在的平面为β,直角坐标系xOy所在的平面为α,且二面角α-y轴-β的大小等于30°.已知β内的曲线C′的方程是3(x-2$\sqrt{3}$)2+4y2-36=0,则曲线C′在α内的射影在坐标系xOy下的曲线方程是(x-3)2+y2=9.
如图,直角坐标系x′Oy所在的平面为β,直角坐标系xOy所在的平面为α,且二面角α-y轴-β的大小等于30°.已知β内的曲线C′的方程是3(x-2$\sqrt{3}$)2+4y2-36=0,则曲线C′在α内的射影在坐标系xOy下的曲线方程是(x-3)2+y2=9.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
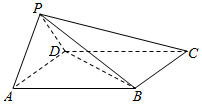 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=$\frac{π}{3}$,△ADP为等边三角形.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=$\frac{π}{3}$,△ADP为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 210-1 | B. | 212-1 | C. | 310-1 | D. | 332-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
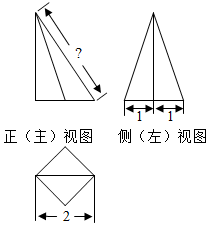 一个底面为正方形的四棱锥,其三视图如图所示,若这个四棱锥的体积为2,则此四棱锥最长的侧棱长为( )
一个底面为正方形的四棱锥,其三视图如图所示,若这个四棱锥的体积为2,则此四棱锥最长的侧棱长为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{11}$ | C. | $\sqrt{13}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}}$) | B. | (${\frac{1}{2}$,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com