
分析 将正四棱锥S-ABCD展开,得到六边形SABCDA'.连结AA',分别交SB、SC、SD于E、F,G,可得截面△AEFG周长的最小值等于线段AA'长,根据余弦定理加以计算,可得答案.
解答 解:将正四棱锥S-ABCD展开,得到六边形SABCDA'.
连结AA',分别交SB、SC、SD于E、F,G
再将展开图围成三棱锥S-ABC的侧面得到△AEF,即为周长最小的截面三角形,
由此可得截面△AEFG周长的最小值等于线段AA'长.
∵正四棱锥S-ABCD侧棱长为4,∠ASB=30°,∴∠ASA'=4×30°=120°.
∴由余弦定理可得AA′=$\sqrt{{4}^{2}+{4}^{2}-2×4×4×(-\frac{1}{2})}$=4$\sqrt{3}$
即截面△AEFG周长的最小值为4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题已知正四棱锥的侧面等腰三角形的顶角,在侧棱长为4的条件下求截面的周长最小值,着重考查了正四棱锥的性质、余弦定理和多面体的侧面展开图等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
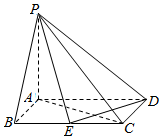 如图四棱锥P-ABCD底面是矩形,PA⊥平面ABCD,PA=AB=1,$BC=\sqrt{2}$,E是BC上的点,
如图四棱锥P-ABCD底面是矩形,PA⊥平面ABCD,PA=AB=1,$BC=\sqrt{2}$,E是BC上的点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
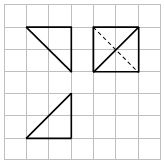
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
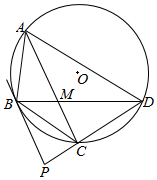 已知四边形ABCD为⊙O的内接四边形,且BC=CD,其对角线AC与BD相交于点M.过点B作⊙O的切线交DC的延长线于点P.
已知四边形ABCD为⊙O的内接四边形,且BC=CD,其对角线AC与BD相交于点M.过点B作⊙O的切线交DC的延长线于点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=4 | B. | m≠4 | C. | m≠-1 | D. | m∈R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com