
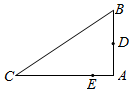
 如图所示,D、E分别是△ABC的边AB、AC上的点(D、E不与边的端点重合).已知线段AD、AB的长分别为m、n,AE、AC的长是关于x的方程x2-18x+mn=0的两个根.
如图所示,D、E分别是△ABC的边AB、AC上的点(D、E不与边的端点重合).已知线段AD、AB的长分别为m、n,AE、AC的长是关于x的方程x2-18x+mn=0的两个根.分析 (1)利用平面几何知识证得△ADE∽△ACB,进一步得到∠ADE=∠ACB,从而得到C、B、D、E四点共圆;
(2)求解方程x2-18x+mn=0的两个根,得到AE=2,AC=16.设所求外接圆的圆心为O,半径为R,则圆心O为线段CE的中垂线与线段BD的中垂线的交点,利用勾股定理求得四边形CBDE外接圆的半径的平方得答案.
解答 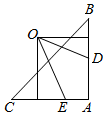 (1)证明:连接DE,根据题意,在△ADE和△ACB中,
(1)证明:连接DE,根据题意,在△ADE和△ACB中,
AD•AB=mn=AE•AC,即$\frac{AD}{AC}=\frac{AE}{AB}$
又∠ADE=∠ACB,∴△ADE∽△ACB,
因此∠ADE=∠ACB,
∴C、B、D、E四点共圆;
(2)解:当m=4,n=8时,方程x2-18x+mn=0的两个根为x1=2,x2=16.
故AE=2,AC=16.
设所求外接圆的圆心为O,半径为R,则圆心O为线段CE的中垂线与线段BD的中垂线的交点,
则|OE|=r,则${r}^{2}=(\frac{16-2}{2})^{2}+(4+\frac{8-4}{2})^{2}=85$.
故四边形CBDE外接圆的面积为85π.
点评 本题考查圆内接多边形性质的判断,考查分析问题和求解问题的能力,属中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | ${A}_{100-n}^{80}$ | B. | ${A}_{100-n}^{21-n}$ | C. | ${A}_{100-n}^{79}$ | D. | ${A}_{100}^{21-n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,直角坐标系x′Oy所在的平面为β,直角坐标系xOy所在的平面为α,且二面角α-y轴-β的大小等于30°.已知β内的曲线C′的方程是3(x-2$\sqrt{3}$)2+4y2-36=0,则曲线C′在α内的射影在坐标系xOy下的曲线方程是(x-3)2+y2=9.
如图,直角坐标系x′Oy所在的平面为β,直角坐标系xOy所在的平面为α,且二面角α-y轴-β的大小等于30°.已知β内的曲线C′的方程是3(x-2$\sqrt{3}$)2+4y2-36=0,则曲线C′在α内的射影在坐标系xOy下的曲线方程是(x-3)2+y2=9.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.过点E的平面α垂直于平面SAC.
已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的任意一点.过点E的平面α垂直于平面SAC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
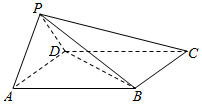 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=$\frac{π}{3}$,△ADP为等边三角形.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=$\frac{π}{3}$,△ADP为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 210-1 | B. | 212-1 | C. | 310-1 | D. | 332-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com