
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在
在![]() 处的切线
处的切线![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)当![]() 时,求证:存在实数
时,求证:存在实数![]() 使
使![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)先根据题意可得![]() 处的切线
处的切线![]() 的斜率为2,从而求得a(2)对于存在问题可根据题意赋值验证,当
的斜率为2,从而求得a(2)对于存在问题可根据题意赋值验证,当![]() 时,显然有
时,显然有![]() ,即存在实数
,即存在实数![]() 使
使![]() ;当
;当![]() 时分析函数单调性,得函数最小值,若最小值小于1即得证
时分析函数单调性,得函数最小值,若最小值小于1即得证
试题解析:
(Ⅰ)![]() ,
,
因为曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,
垂直,
所以切线![]() 的斜率为2,
的斜率为2,
所以![]() ,
,
所以![]() .
.
(Ⅱ)法1:当![]() 时,显然有
时,显然有![]() ,即存在实数
,即存在实数![]() 使
使![]() ;
;
当![]() 时,由
时,由![]() 可得
可得![]() ,
,
所以在![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上递减;
上递减;
![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上递增
上递增
所以![]()
![]() 是
是![]() 的极小值.
的极小值.
由函数![]() 可得
可得![]() ,
,
由![]() 可得
可得![]() ,
,
所以![]() ,
,
综上,若![]() ,存在实数
,存在实数![]() 使
使![]() .
.
(Ⅱ)法2:当![]() 时,显然有
时,显然有![]() ,即存在实数
,即存在实数![]() 使
使![]() ;
;
当![]() 时,由
时,由![]() 可得
可得![]() ,
,
所以在![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上递减;
上递减;
![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在
在![]() 上递增.
上递增.
所以![]()
![]() 是
是![]() 的极小值.
的极小值.
设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]()
|
|
|
|
| + | 0 | - |
| ↗ | 极大值 | ↘ |
所以当![]() 时
时![]() ,
,
所以![]() ,
,
综上,若![]() ,存在实数
,存在实数![]() 使
使![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
【题目】若函数![]() 在实数集
在实数集![]() 上的图象是连续不断的,且对任意实数
上的图象是连续不断的,且对任意实数![]() 存在常数
存在常数![]() 使得
使得![]() 恒成立,则称
恒成立,则称![]() 是一个“关于
是一个“关于![]() 函数”.现有下列“关于
函数”.现有下列“关于![]() 函数”的结论:
函数”的结论:
①常数函数是“关于![]() 函数”;
函数”;
②正比例函数必是一个“关于![]() 函数”;
函数”;
③“关于![]() 函数”至少有一个零点;
函数”至少有一个零点;
④![]() 是一个“关于
是一个“关于![]() 函数”.
函数”.
其中正确结论的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,点![]() (n∈N*)均在函数y=3x-2的图象上.
(n∈N*)均在函数y=3x-2的图象上.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以![]() 为组距分成
为组距分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
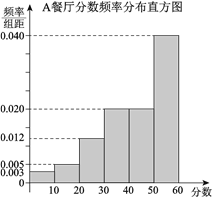
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
定义学生对餐厅评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 |
|
|
|
(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为![]() 的人数;
的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={1,2,3},集合B={x|a+1<x<6a﹣1},其中a∈R.
(1)写出集合A的所有真子集;
(2)若A∩B={3},求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某钢厂打算租用![]() ,
, ![]() 两种型号的火车车皮运输900吨钢材,
两种型号的火车车皮运输900吨钢材, ![]() ,
, ![]() 两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且
两种车皮的载货量分别为36吨和60吨,租金分别为1.6万元/个和2.4万元/个,钢厂要求租车皮总数不超过21个,且![]() 型车皮不多于
型车皮不多于![]() 型车皮7个,分别用
型车皮7个,分别用![]() ,
, ![]() 表示租用
表示租用![]() ,
, ![]() 两种车皮的个数.
两种车皮的个数.
(Ⅰ)用![]() ,
, ![]() 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;
(Ⅱ)分别租用![]() ,
, ![]() 两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
两种车皮的个数是多少时,才能使得租金最少?并求出此最小租金.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com