
 在一圆柱中挖去一圆锥所得的机械部件的三视图如图所示,则此机械部件的表面积为( )
在一圆柱中挖去一圆锥所得的机械部件的三视图如图所示,则此机械部件的表面积为( )| A. | (7+$\sqrt{2}$)π | B. | (8+$\sqrt{2}$)π | C. | $\frac{22π}{7}$ | D. | (1+$\sqrt{2}$)π+6 |
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:解答题
 如图,已知抛物线C1:y2=4x的焦点为F,椭圆C2的中心在原点,F为其右焦点,点M为曲线C1和C2在第一象限的交点,且|$\overrightarrow{MF}$|=$\frac{5}{2}$.
如图,已知抛物线C1:y2=4x的焦点为F,椭圆C2的中心在原点,F为其右焦点,点M为曲线C1和C2在第一象限的交点,且|$\overrightarrow{MF}$|=$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
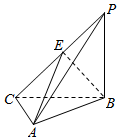 如图,三棱锥P-ABC中,PB⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC的中点.
如图,三棱锥P-ABC中,PB⊥平面ABC,PB=BC=CA=4,∠BCA=90°,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
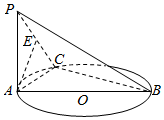 如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点,$AB=\sqrt{3}$,PA=AC=1.
如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点,$AB=\sqrt{3}$,PA=AC=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com