
分析 (1)利用平面向量的坐标运算与向量相等,求出μ的表达式,再利用三角函数的恒等变换求出μ的取值范围;
(2)根据λ与μ的关系求出$\frac{{λ}^{2}}{μ}$的表达式,利用μ的取值范围和函数的单调性即可求出$\frac{{λ}^{2}}{μ}$的取值范围.
解答 解:(1)向量$\overrightarrow a=(λ,{λ^2}-{sin^2}α)$,$\overrightarrow b=(μ-1,μ+cosα)$,
∴-2$\overrightarrow{b}$=(-2μ+2,-2μ-2cosα);
又$\overrightarrow a=-2\overrightarrow b$,
∴$\left\{\begin{array}{l}{λ=-2μ+2}\\{{λ}^{2}{-sin}^{2}α=-2μ-2cosα}\end{array}\right.$,
∴(-2μ+2)2-sin2α=-2μ-2cosα,
化简得4μ2-6μ+4=sin2α-2cosα;
设t=sin2α-2cosα,
则t=1-cos2α-2cosα=-(cosα+1)2+2;
由-1≤cosα≤1,求得-2≤t≤2;
∴-2≤4μ2-6μ+4≤2,
即-1≤2μ2-3μ+2≤1,
解得$\frac{1}{2}≤μ≤1$;
(2)∵λ=-2μ+2,
∴$\frac{{λ}^{2}}{μ}$=$\frac{{(-2μ+2)}^{2}}{μ}$=$\frac{{4μ}^{2}-8μ+4}{μ}$=4μ+$\frac{4}{μ}$-8,
又$\frac{1}{2}$≤μ≤1时,函数t=4μ+$\frac{4}{μ}$是单调减函数;
当u=$\frac{1}{2}$时,函数t=2+8=10为最大值,
当μ=1时,函数t=4+4=8为最小值;
所以8-8≤4μ+$\frac{4}{μ}$-8≤10-8,
即0≤$\frac{{λ}^{2}}{μ}$≤2.
点评 本题考查了平面向量的坐标运算与向量相等,以及三角函数的性质与应用问题,是综合性题目.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{2}{\sqrt{3}}$ | D. | ±$\frac{2}{\sqrt{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
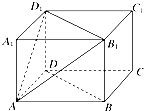 如图,在长方体ABCD-A1B1C1D1中,AB=AD=4cm,AA1=2cm,设平面AB1D1与平面ABCD所成二面角为θ,tanθ=$\frac{1}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=4cm,AA1=2cm,设平面AB1D1与平面ABCD所成二面角为θ,tanθ=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com