
若两条异面直线所成的角为 ,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有( )
,则称这对异面直线为“黄金异面直线对”,在连接正方体各顶点的所有直线中,“黄金异面直线对”共有( )
A.12对 B.18对 C.24 对 D.30对
科目:高中数学 来源:2013-2014学年甘肃省张掖市高三第三次诊断考试文科数学试卷(解析版) 题型:解答题
已知椭圆 的离心率为
的离心率为 ,以原点
,以原点 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线 相切。
相切。
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线 与椭圆
与椭圆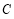 相交于
相交于 、
、 两点,且
两点,且 ,试判断
,试判断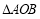 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省长沙市高考二模理科数学试卷(解析版) 题型:解答题
已知A、B为抛物线C:y2 = 4x上的两个动点,点A在第一象限,点B在第四象限l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.
(1)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;
(2)设C、D为直线l1、l2与直线x = 4的交点,求 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省长沙市高考二模理科数学试卷(解析版) 题型:填空题
设点P是双曲线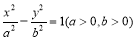 与圆x2+y2=a2+b2在第一象限的交点,其中F1,F2分别是双曲线的左、右焦点,且
与圆x2+y2=a2+b2在第一象限的交点,其中F1,F2分别是双曲线的左、右焦点,且 ,则双曲线的离心率为______.[来
,则双曲线的离心率为______.[来
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省长沙市高考二模理科数学试卷(解析版) 题型:选择题
设A,B为两个互不相同的集合,命题P: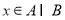 , 命题q:
, 命题q: 或
或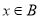 ,则
,则 是
是 的( )
的( )
A.充分且必要条件 B.充分非必要条件
C.必要非充分条件 D.非充分且非必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省长沙市高考二模文科数学试卷(解析版) 题型:解答题
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB= 60°,FC⊥平面ABCD,AE⊥BD,CB= CD= CF.
(1)求证:BD⊥平面AED;
(2)求二面角F—BD—C的正切值.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省长沙市高考二模文科数学试卷(解析版) 题型:选择题
已知集合 ,则
,则 等于( )
等于( )
A.{-1,0,1} B.{1} C.{-1,1} D.{0,1}
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南省益阳市高三模拟考试文科数学试卷(解析版) 题型:选择题
某工厂有甲、乙、丙三类产品,其数量之比为 ,现要用分层抽样的方法从中抽取
,现要用分层抽样的方法从中抽取 件产品进行质量检测,则乙类产品应抽取的件数为( )
件产品进行质量检测,则乙类产品应抽取的件数为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com