
【题目】已知曲线![]() 和曲线
和曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,且两种坐标系中取相同的单位长度.
轴正半轴为极轴,建立极坐标系,且两种坐标系中取相同的单位长度.
(1)求曲线![]() 和曲线
和曲线![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,若射线
,若射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,求
,求![]() 两点间的距离.
两点间的距离.
【答案】(1)![]() ;(2)1.
;(2)1.
【解析】
(1)利用x=ρcosθ,y=ρsinθ,将普通方程化为极坐标方程即可;(2)求出M,N,P的坐标,得到射线的极坐标方程,分别代入C1、C2得到,P,Q的极坐标,求距离即可.
(1)线C1:x![]() y
y![]() 和C2:
和C2:![]() (φ为参数),以原点O为极点,x 轴的正半轴为极轴,建立极坐标系,因为x=ρcosθ,y=ρsinθ,
(φ为参数),以原点O为极点,x 轴的正半轴为极轴,建立极坐标系,因为x=ρcosθ,y=ρsinθ,
所以C1:![]() ,即
,即![]() ,所以
,所以![]() ;
;
C2的普通方程为![]() ,所以其极坐标方程为
,所以其极坐标方程为![]() ,即
,即![]() .
.
(2)由题意M(![]() ,0),N(0,1),所以P(
,0),N(0,1),所以P(![]() ),所以射线OP的极坐标方程为:
),所以射线OP的极坐标方程为:![]() ,把
,把![]() 代入C1得到ρ1=1,P(1,
代入C1得到ρ1=1,P(1,![]() );
);
把![]() 代入C2得到ρ2=2,Q(2,
代入C2得到ρ2=2,Q(2,![]() ),
),
所以|PQ|=|ρ2﹣ρ1|=1,即P,Q两点间的距离为1.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,焦距为6.
,焦距为6.
(1)求椭圆![]() 的方程.
的方程.
(2)过椭圆左顶点的两条斜率之积为![]() 的直线分别与椭圆交于
的直线分别与椭圆交于![]() 点.试问直线
点.试问直线![]() 是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上的动点,
是椭圆上的动点,![]() 的面积的最大值为
的面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() ,线段
,线段![]() 的中垂线为
的中垂线为![]() .若直线
.若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市收集并整理了该市2017年1月份至10月份每月份最低气温与最高气温(单位:![]() )的数据,绘制了折线图(如图).已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系,则根据该折线图,下列结论错误的是()
)的数据,绘制了折线图(如图).已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系,则根据该折线图,下列结论错误的是()
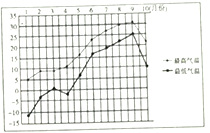
A. 最低气温低于![]() 的月份有
的月份有![]() 个
个
B. ![]() 月份的最高气温不低于
月份的最高气温不低于![]() 月份的最高气温
月份的最高气温
C. 月温差(最高气温减最低气温)的最大值出现在![]() 月份
月份
D. 每月份最低气温与当月的最高气温两变量为正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3,4五个数中任取的一个数,
是从0,1,2,3,4五个数中任取的一个数,![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数,![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,错误的是( )
A.圆锥所有的轴截面是全等的等腰三角形
B.圆柱的轴截面是过母线的截面中面积最大的一个
C.圆锥的轴截面是所有过顶点的界面中面积最大的一个
D.当球心到平面的距离小于球面半径时,球面与平面的交线总是一个圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线![]()
![]() 的焦点,过F且倾斜角为
的焦点,过F且倾斜角为![]() 的直线交抛物线于A,B两点,
的直线交抛物线于A,B两点,![]() .
.
(1)求抛物线的方程:
(2)已知![]() 为抛物线上一点,M,N为抛物线上异于P的两点,且满足
为抛物线上一点,M,N为抛物线上异于P的两点,且满足![]() ,试探究直线MN是否过一定点?若是,求出此定点;若不是,说明理由.
,试探究直线MN是否过一定点?若是,求出此定点;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com