练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

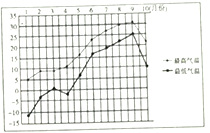
    【题目】某城市收集并整理了该市2017年1月份至10月份每月份最低气温与最高气温（单位：）的数据，绘制了折线图（如图）.已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系，则根据该折线图，下列结论错误的是（）

    A. 最低气温低于的月份有个

    B. 月份的最高气温不低于月份的最高气温

    C. 月温差（最高气温减最低气温）的最大值出现在月份

    D. 每月份最低气温与当月的最高气温两变量为正相关

    【答案】A

    【解析】

    由该市2017年1月份至10月份各月最低气温与最高气温（单位：℃）的数据的折线图，得最低气温低于0℃的月份有3个．

    由该市2017年1月份至10月份各月最低气温与最高气温（单位：℃）的数据的折线图，得：在A中，最低气温低于0℃的月份有3个，故A错误．

    在B中，10月的最高气温不低于5月的最高气温，故B正确；

    在C中，月温差（最高气温减最低气温）的最大值出现在1月，故C正确；

    在D中，最低气温与最高气温为正相关，故D正确；

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，，是抛物线上的两个动点，且，过，两点分别作抛物线的切线，设其交点为.

    （1）若直线与，轴分别交于点，，且的面积为，求的值；

    （2）记的面积为，求的最小值，并指出最小时对应的点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】东方商店欲购进某种食品（保质期一天），此商店每两天购进该食品一次（购进时，该食品为刚生产的）.根据市场调查，该食品每份进价元，售价元，如果一天内无法售出，则食品过期作废，现统计该产品天的销售量如下表：

    （1）根据该产品天的销售量统计表，求平均每天销售多少份？

    （2）视样本频率为概率，以一天内该产品所获得的利润的平均值为决策依据，东方商店一次性购进或份，哪一种得到的利润更大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】抛物线的准线与轴交于点，过点作直线交抛物线于，两点.

    （1）求直线的斜率的取值范围；

    （2）若线段的垂直平分线交轴于，求证：；

    （3）若直线的斜率依次为，，，…，，…，线段的垂直平分线与轴的交点依次为，，，…，，…，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线和曲线（为参数），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，且两种坐标系中取相同的单位长度.

    （1）求曲线和曲线的极坐标方程；

    （2）设曲线与轴、轴分别交于两点，且线段的中点为，若射线与曲线交于点，求两点间的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱锥P-ABC的三条侧棱两两互相垂直，且AB=，BC=，AC=2，则此三棱锥外接球的表面积为______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为，且椭圆上存在一点，满足.

    （1）求椭圆的标准方程；

    （2）过椭圆右焦点的直线与椭圆交于不同的两点，求的内切圆的半径的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）当时，讨论函数的单调性；

    （Ⅱ）当，时，，其中，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着计算机的出现，图标被赋予了新的含义，又有了新的用武之地.在计算机应用领域，图标成了具有明确指代含义的计算机图形.如图所示的图标是一种被称之为“黑白太阳”的图标，该图标共分为3部分.第一部分为外部的八个全等的矩形，每一个矩形的长为3、宽为1；第二部分为圆环部分，大圆半径为3，小圆半径为2；第三部分为圆环内部的白色区域.在整个“黑白太阳”图标中随机取一点，则此点取自图标第三部分的概率为（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案