
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() ,
,![]() 是抛物线上的两个动点,且
是抛物线上的两个动点,且![]() ,过
,过![]() ,
,![]() 两点分别作抛物线的切线,设其交点为
两点分别作抛物线的切线,设其交点为![]() .
.
(1)若直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,求
,求![]() 的值;
的值;
(2)记![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值,并指出
的最小值,并指出![]() 最小时对应的点
最小时对应的点![]() 的坐标.
的坐标.
科目:高中数学 来源: 题型:
【题目】祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高。这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。设由椭圆![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知抛物线C:x2=4y的焦点为F,直线l与抛物线C交于A,B两点,延长AF交抛物线C于点D,若AB的中点纵坐标为|AB|-1,则当∠AFB最大时,|AD|=( )
A. 4B. 8C. 16D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知棱柱![]() 的底面是菱形,且
的底面是菱形,且![]() 面ABCD,
面ABCD,![]() ,F为棱
,F为棱![]() 的中点,M为线段
的中点,M为线段![]() 的中点.
的中点.
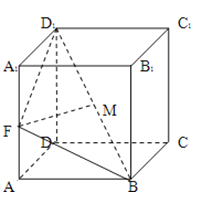
(1)求证:![]() 面ABCD;
面ABCD;
(2)判断直线MF与平面![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,焦距为6.
,焦距为6.
(1)求椭圆![]() 的方程.
的方程.
(2)过椭圆左顶点的两条斜率之积为![]() 的直线分别与椭圆交于
的直线分别与椭圆交于![]() 点.试问直线
点.试问直线![]() 是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为改善人居环境,某区增加了对环境综合治理的资金投入,已知今年治理环境![]() (亩)与相应的资金投入
(亩)与相应的资金投入![]() (万元)的四组对应数据的散点图如图所示,用最小二乘法得到
(万元)的四组对应数据的散点图如图所示,用最小二乘法得到![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
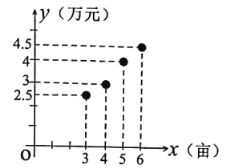
(1)求![]() 的值,并预测今年治理环境10亩所需投入的资金是多少万元?
的值,并预测今年治理环境10亩所需投入的资金是多少万元?
(2)已知该区去年治理环境10亩所投入的资金为3.5万元,根据(1)的结论,请你对该区环境治理给出一条简短的评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,线段
的中点,线段![]() 与
与![]() 交于
交于![]() 点(如图1).将
点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得二面角
的位置,使得二面角![]() 为直二面角(如图2).
为直二面角(如图2).
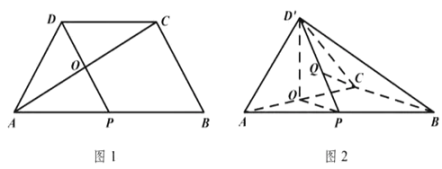
(1)求证:![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄(单位:岁)分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)请根据频率分布直方图,估计这100名志愿者样本的平均数;
(3)在(1)的条件下,该市决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.(参考数据:![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市收集并整理了该市2017年1月份至10月份每月份最低气温与最高气温(单位:![]() )的数据,绘制了折线图(如图).已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系,则根据该折线图,下列结论错误的是()
)的数据,绘制了折线图(如图).已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系,则根据该折线图,下列结论错误的是()
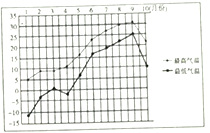
A. 最低气温低于![]() 的月份有
的月份有![]() 个
个
B. ![]() 月份的最高气温不低于
月份的最高气温不低于![]() 月份的最高气温
月份的最高气温
C. 月温差(最高气温减最低气温)的最大值出现在![]() 月份
月份
D. 每月份最低气温与当月的最高气温两变量为正相关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com