练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】己知抛物线C：x2=4y的焦点为F，直线l与抛物线C交于A，B两点，延长AF交抛物线C于点D，若AB的中点纵坐标为|AB|-1，则当∠AFB最大时，|AD|=（　　）

    A. 4B. 8C. 16D.

    【答案】C

    【解析】

    设出A，B，D的坐标，利用抛物线定义可得|AF|+|BF|=2|AB|，再由余弦定理写出cos∠AFB，利用基本不等式求最值，可得当∠AFB最大时，△AEB为等边三角形，得到AF所在直线方程，再与抛物线方程联立，结合根与系数的关系及抛物线定义求得|AD|．

    解：

    设A（x1，y1），B（x2，y2），D（x3，y3），

    由抛物线定义得：y1+y2+2=|AF|+|BF|，

    ，

    ，当且仅当|AF|=|BF|时取等号．

    ∴当∠AFB最大时，△AFB为等边三角形，

    联立 ，，消去y，得．

    ．

    ∴|AD|=16．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知，对于，均有，则实数的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4—4：坐标系与参数方程

    在平面直角坐标系中，直线的参数方程为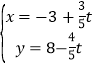（为参数），圆的方程为．以原点为极点，轴正半轴为极轴建立极坐标系．

    （Ⅰ）求直线及圆的极坐标方程；

    （Ⅱ）若直线与圆交于，两点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知为坐标原点，抛物线：与直线：交于点，两点，且.

    （1）求抛物线的方程；

    （2）线段的中点为，过点且斜率为的直线交抛物线于，两点，若直线，分别与直线交于，两点，当时，求斜率的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列有关平面向量分解定理的四个命题：

    （1）一个平面内有且只有一对不平行的向量可作为表示该平面所有向量的基；

    （2）一个平面内有无数多对不平行向量可作为表示该平面内所有向量的基；

    （3）平面向量的基向量可能互相垂直；

    （4）一个平面内任一非零向量都可唯一地表示成该平面内三个互不平行向量的线性组合.

    其中正确命题的个数是（ ）

    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线:，抛物线图象上的一动点到直线与到轴距离之和的最小值为__________，到直线距离的最小值为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，已知曲线C的参数方程为（α为参数，直线l：y=kx（k＞0），以O为极点，x轴正半轴为极轴建立极坐标系．

    （Ⅰ）求曲线C的极坐标方程；

    （Ⅱ）若直线l与曲线C交于A，B两点，求|OA||OB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，，是抛物线上的两个动点，且，过，两点分别作抛物线的切线，设其交点为.

    （1）若直线与，轴分别交于点，，且的面积为，求的值；

    （2）记的面积为，求的最小值，并指出最小时对应的点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】东方商店欲购进某种食品（保质期一天），此商店每两天购进该食品一次（购进时，该食品为刚生产的）.根据市场调查，该食品每份进价元，售价元，如果一天内无法售出，则食品过期作废，现统计该产品天的销售量如下表：

    （1）根据该产品天的销售量统计表，求平均每天销售多少份？

    （2）视样本频率为概率，以一天内该产品所获得的利润的平均值为决策依据，东方商店一次性购进或份，哪一种得到的利润更大？

    查看答案和解析>>

    同步练习册答案