
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为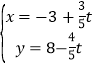 (
(![]() 为参数),圆
为参数),圆![]() 的方程为
的方程为![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(Ⅰ)求直线![]() 及圆
及圆![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
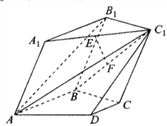
【题目】在如图所示的多面体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为边长为2的菱形,
为边长为2的菱形, ![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为平行四边形,且
为平行四边形,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
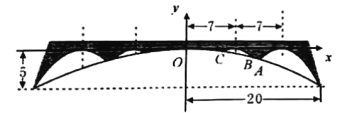
【题目】早在一千多年之前,我国已经把溢流孔用于造桥技术,以减轻桥身重量和水流对桥身的冲击,现设桥拱上有如图所示的4个溢流孔,桥拱和溢流孔轮廓线均为抛物线的一部分,且四个溢流孔轮廓线相同.根据图上尺寸,在平面直角坐标系![]() 中,桥拱所在抛物线的方程为_______,溢流孔与桥拱交点
中,桥拱所在抛物线的方程为_______,溢流孔与桥拱交点![]() 的坐标为_______.
的坐标为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高。这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。设由椭圆![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥S-ABCD中,底面ABCD为长方形,![]() 底面
底面![]() ,其中
,其中![]() ,
,![]() ,
,![]() 的可能取值为:①
的可能取值为:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]()
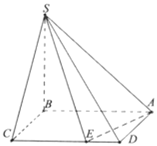
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若线段CD上能找到点E,满足![]() 的点有两个,分别记为
的点有两个,分别记为![]() ,
,![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】前些年有些地方由于受到提高![]() 的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭、整顿,另一方面进行大量的绿化来净化和吸附污染物.通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭、整顿,另一方面进行大量的绿化来净化和吸附污染物.通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
(1)某机构随机访问50名居民,这50名居民对政府的评分(满分100分)如下表:
分数 |
|
|
|
|
|
|
频数 | 2 | 3 | 11 | 14 | 11 | 9 |
请在答题卡上作出居民对政府的评分频率分布直方图:
(2)当地环保部门随机抽测了2018年11月的空气质量指数,其数据如下表:
空气质量指数( | 0-50 | 50-100 | 100-150 | 150-200 |
天数 | 2 | 18 | 8 | 2 |
用空气质量指数的平均值作为该月空气质量指数级别,求出该月空气质量指数级别为第几级?(同一组数据用该组数据的区间中点值作代表,将频率视为概率)(相关知识参见附表)
(3)空气受到污染,呼吸系统等疾病患者最易感染,根据历史经验,凡遇到空气轻度污染,小李每天会服用有关药品,花费50元,遇到中度污染每天服药的费用达到100元.环境整治前的2015年11月份小李因受到空气污染患呼吸系统等疾病花费了5000元,试估计2018年11月份(参考(2)中表格数据)小李比以前少花了多少钱的医药费?
附:
空气质量指数( | 0-50 | 50-100 | 100-150 | 150-200 | 200-300 |
|
空气质量指数级别 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
空气质量指数 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】历史上数列的发展,折射出许多有价值的数学思想方法,对时代的进步起了重要的作用,比如意大利数学家列昂纳多·斐波那契以兔子繁殖为例,引入“兔子数列”:即1,1,2,3,5,8,13,21,34,55,89,144,233,….即![]() ,
,![]() ,此数列在现代物理、准晶体结构及化学等领域有着广泛的应用,若此数列被4整除后的余数构成一个新的数列
,此数列在现代物理、准晶体结构及化学等领域有着广泛的应用,若此数列被4整除后的余数构成一个新的数列![]() ,又记数列
,又记数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知抛物线C:x2=4y的焦点为F,直线l与抛物线C交于A,B两点,延长AF交抛物线C于点D,若AB的中点纵坐标为|AB|-1,则当∠AFB最大时,|AD|=( )
A. 4B. 8C. 16D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,线段
的中点,线段![]() 与
与![]() 交于
交于![]() 点(如图1).将
点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得二面角
的位置,使得二面角![]() 为直二面角(如图2).
为直二面角(如图2).
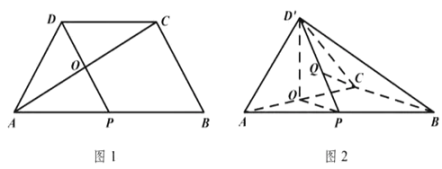
(1)求证:![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com