Question

16．在△ABC中，内角A、B、C所对的边分别为a、b、c，已知c²sinAcosA+a²sinCcosC=4sinB，cosB=$\frac{\sqrt{7}}{4}$，D是AC上一点，且S_△BCD=$\frac{2}{3}$，则$\frac{AD}{AC}$等于（　　）

• A． $\frac{3}{7}$
• B． $\frac{1}{2}$
• C． $\frac{5}{8}$
• D． $\frac{5}{9}$

Answer 1

分析 由正弦宣理得ac=$\frac{4b}{ccosA+acosC}$，再由余弦定理得到ac=4，从而求出△ABC的面积，进而求出△ABD的面积，由$\frac{AD}{AC}$=$\frac{{S}_{△ABD}}{{S}_{△ABC}}$能求出结果．

解答 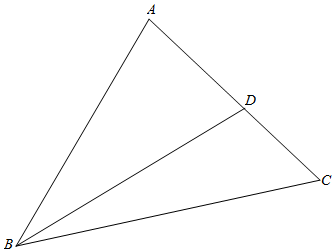解：∵在△ABC中，内角A、B、C所对的边分别为a、b、c，
c²sinAcosA+a²sinCcosC=4sinB，
∴c²acosA+a²ccosC=4b，
∴ac=$\frac{4b}{ccosA+acosC}$
=$\frac{4b}{c×\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}+a×\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}}$
=$\frac{8{b}^{2}}{2{b}^{2}}$=4，
∵cosB=$\frac{\sqrt{7}}{4}$，∴sinB=$\frac{3}{4}$，
∴${S}_{△ABC}=\frac{1}{2}acsinB$=$\frac{1}{2}×4×\frac{3}{4}$=$\frac{3}{2}$，
∵D是AC上一点，且S_△BCD=$\frac{2}{3}$，∴${S}_{△ABD}=\frac{3}{2}-\frac{2}{3}$=$\frac{5}{6}$，
∴$\frac{AD}{AC}$=$\frac{{S}_{△ABD}}{{S}_{△ABC}}$=$\frac{\frac{5}{6}}{\frac{3}{2}}$=$\frac{5}{9}$．
故选：D．

点评 本题考查三角形两线段比值的求法，考查正弦定理、余弦定理、三角形面积公式等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．