
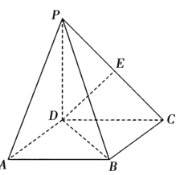
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() 为
为![]() 中点,
中点,![]() .
.

(1)求证:![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由面面垂直的性质定理可得出![]() 平面
平面![]() ,可得出
,可得出![]() ,由等腰三角形三线合一的性质可得出
,由等腰三角形三线合一的性质可得出![]() ,由此可得出
,由此可得出![]() 平面
平面![]() ,进而得出
,进而得出![]() ;
;
(2)设![]() ,可得出
,可得出![]() ,
,![]() ,由(1)可知,
,由(1)可知,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,可得
,可得![]() ,进而以点
,进而以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,利用空间向量法可求出二面角
轴建立空间直角坐标系,利用空间向量法可求出二面角![]() 的大小.
的大小.
(1)![]() 四边形
四边形![]() 为矩形,则
为矩形,则![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 面
面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() ;
;
(2)不妨设![]() ,由
,由![]() 得
得![]() ,由(1)得
,由(1)得![]() ,∴
,∴![]() ,∴
,∴![]() ,由(1)得
,由(1)得![]() 平面
平面![]() ,
,
由(1)知,![]() 在平面
在平面![]() 的射影为
的射影为![]() ,即
,即![]() ,
,
![]() ,故
,故![]() .
.
以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立如下图所示的空间直角坐标系
轴建立如下图所示的空间直角坐标系![]() ,
,
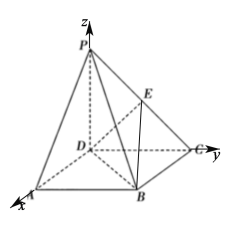
易得![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 与平面
与平面![]() 的法向量分别为
的法向量分别为![]() 和
和![]() ,
,
则![]() ,
,
由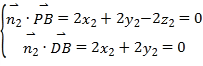 ,令
,令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
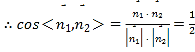 ,设二面角
,设二面角![]() 的大小为
的大小为![]() ,则
,则![]() ,所以二面角
,所以二面角![]() 的大小
的大小![]()


科目:高中数学 来源: 题型:
【题目】2016年1月14日,国防科工局宣布,嫦娥四号任务已经通过了探月工程重大专项领导小组审议通过,正式开始实施.如图所示,假设“嫦娥四号”卫星将沿地月转移轨道飞向月球后,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行.若用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用
分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用![]() 和
和![]() 分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,给出下列式子:①
分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,给出下列式子:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确式子的序号是( )
.其中正确式子的序号是( )

A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在水平地面上的不同两点处栽有两根笔直的电线杆,假设它们都垂直于地面,则在水平地面上视它们上端仰角相等的点![]() 的轨迹可能是( )
的轨迹可能是( )
①直线 ②圆 ③椭圆 ④抛物线
A.①②B.①③C.①②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 与
与![]() 的交点的直角坐标;
的交点的直角坐标;
(2)求![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,上、下顶点分别为
,上、下顶点分别为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试探究在
两点,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得可
,使得可![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标,若不存在,请说明理由?
的坐标,若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知平行于
中,已知平行于![]() 轴的动直线
轴的动直线![]() 交抛物线
交抛物线![]() :
: ![]() 于点
于点![]() ,点
,点![]() 为
为![]() 的焦点.圆心不在
的焦点.圆心不在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() ,
, ![]() ,
, ![]() 轴都相切,设
轴都相切,设![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,过
,过![]() 且垂直于
且垂直于![]() 的直线为
的直线为![]() ,直线
,直线![]() ,
, ![]() 分别与
分别与![]() 轴相交于点
轴相交于点![]() ,
, ![]() .当线段
.当线段![]() 的长度最小时,求
的长度最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,(x>0).
,(x>0).
(1)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(2)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(3)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb](m≠0),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学老师给出一个函数![]() ,甲、乙、丙、丁四个同学各说出了这个函数的一条性质:甲:在
,甲、乙、丙、丁四个同学各说出了这个函数的一条性质:甲:在![]() 上函数单调递减;乙:在
上函数单调递减;乙:在![]() 上函数单调递增;丙:在定义域R上函数的图象关于直线
上函数单调递增;丙:在定义域R上函数的图象关于直线![]() 对称;丁:
对称;丁:![]() 不是函数的最小值.老师说:你们四个同学中恰好有三个人说的正确.那么,你认为____说的是错误的.
不是函数的最小值.老师说:你们四个同学中恰好有三个人说的正确.那么,你认为____说的是错误的.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校将甲、乙等6名新招聘的老师分配到4个不同的年级,每个年级至少分配1名教师,且甲、乙两名老师必须分到同一个年级,则不同的分法种数为______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com