
| A�� | ��0��2�� | B�� | ��0��0�� | C�� | ��4��6�� | D�� | ��2��0�� |
���� ��������ƽ�����Ӷ�����$\overrightarrow{OP}$•$\overrightarrow{OM}$=��$\frac{1}{a}$��$\frac{1}{b}$��•��x��y��=$\frac{x}{a}$+$\frac{y}{b}$���Ӷ�ȷ�����ֵʱ�ĵ㼴�ɣ�
��� �⣺��������ƽ���������£�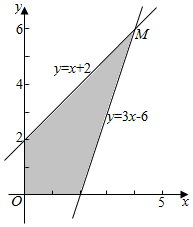 ��
��
$\overrightarrow{OP}$•$\overrightarrow{OM}$=��$\frac{1}{a}$��$\frac{1}{b}$��•��x��y��=$\frac{x}{a}$+$\frac{y}{b}$��
�ʵ�x��y�������ֵʱ��
��x=4��y=6ʱ�������ֵ��
��ѡC��
���� ���⿼�������Թ滮�Ľⷨ�����ν�ϵ�˼�뷽��Ӧ�ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{\sqrt{3}}{3}$ | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x+$\frac{��}{3}$�����溯�� | B�� | f��x+$\frac{��}{3}$����ż���� | C�� | f��x-$\frac{��}{3}$�����溯�� | D�� | f��x-$\frac{��}{3}$����ż���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | n2-1 | B�� | n2 | C�� | n2+1 | D�� | ��n+1��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\frac{\sqrt{2}}{3}$ | D�� | $\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com