
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
分析 法1.取A1C1的中点D,连接DM,则∠MAD是AM与平面AA1C1C所的成角,
法2:以C1点坐标原点,C1A1,C1B1,C1C分别为X,Y,Z轴正方向建立空间坐标系,分另求出直线AM的方向向量与平面AA1C1C的法向量,代入向量夹角公式,即可求出AM与平面AA1C1C所成角的正切值.
解答 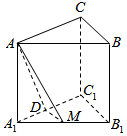 解:法1:取A1C1的中点D,连接DM,
解:法1:取A1C1的中点D,连接DM,
则DM∥C1B1,
在在直三棱柱中,∠ACB=90°,
∴DM⊥平面AA1C1C,
则∠MAD是AM与平面AA1C1C所的成角,
则DM=$\frac{1}{2}$,AD=$\sqrt{(\sqrt{2})^{2}+(\frac{1}{2})^{2}}$=$\sqrt{\frac{9}{4}}$=$\frac{3}{2}$,
则tan∠MAD=$\frac{DM}{AD}=\frac{\frac{1}{2}}{\frac{3}{2}}=\frac{1}{3}$.
法2:以C1点坐标原点,C1A1,C1B1,C1C分别为X,Y,Z轴正方向建立空间坐标系,
则∵AC=BC=1,侧棱AA1=$\sqrt{2}$,M为A1B1的中点,
∴$\overrightarrow{AM}$=(-$\frac{1}{2}$,$\frac{1}{2}$,-$\sqrt{2}$),$\overrightarrow{BC}$=(0,-1,0)为平面AA1C1C的一个法向量
设AM与平面AA1C1C所成角为θ
则sinθ=|$\frac{\overrightarrow{AM}•\overrightarrow{BC}}{\left|\overrightarrow{AM}\right|•\left|\overrightarrow{BC}\right|}$|=$\frac{\sqrt{10}}{10}$
则tanθ=$\frac{1}{3}$
故选:A
点评 本题考查的知识点是直线与平面所成的角,其中利用定义法以及建立坐标系,求出直线的方向向量和平面的法向量,将线面夹角问题转化为向量夹角问题是解答本题的关键.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,0) | C. | (4,6) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则在该几何体中,最长的棱的长度是( )| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 6 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
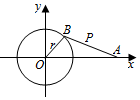 如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.
如图,OB是机器的曲柄,长是r,绕点O转动,AB是连杆,长为l,点A在直线Ox上往返运动,点P是AB的中点,当点B绕点O作圆周运动,求点P的轨迹的参数方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com