
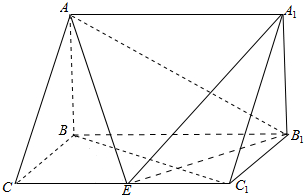
 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,BC=1,BB1=2,AB=$\sqrt{2}$,∠BCC1=$\frac{π}{3}$.分析 (Ⅰ)由余弦定理即可求出${C}_{1}B=\sqrt{3}$,从而可说明C1B⊥BC,而由AB⊥平面BB1C1C可得到EB1⊥AB,从而根据线面垂直的判定定理即可得到C1B⊥平面ABC;
(Ⅱ)连接BE,由上面知EB1⊥BE,设CE=x,(0<x<2),分别根据余弦定理可得到$B{E}^{2},E{{B}_{1}}^{2}$,从而根据$B{E}^{2}+E{{B}_{1}}^{2}=B{{B}_{1}}^{2}$即可求出x=1,从而E点的位置为棱CC1的中点;
(Ⅲ)容易说明∠BAE等于二面角A-EB1-A1平面角的大小,并且△ABE是直角三角形,$BE=1,AB=\sqrt{2}$,从而便能求出二面角A-EB1-A1的正切值.
解答 解:(Ⅰ)证明:△BCC1中,BC=1,CC1=BB1=2,$∠BC{C}_{1}=\frac{π}{3}$;
∴由余弦定理:$B{{C}_{1}}^{2}=1+4-2=3$;
∴$B{C}_{1}=\sqrt{3}$;
∴$B{C}^{2}+B{{C}_{1}}^{2}=C{{C}_{1}}^{2}$;
∴C1B⊥BC;
又AB⊥平面BB1C1C,C1B?平面BB1C1C;
∴C1B⊥AB,AB∩BC=B;
∴C1B⊥平面ABC;
(Ⅱ)如图,连接BE,AB⊥平面BB1C1C;
∴EB1⊥AB;
若EA⊥EB1,即EB1⊥EA,AB∩EA=A;
∴EB1⊥平面ABE,BE?平面ABE;
∴EB1⊥BE;
设CE=x.则EC1=2-x;
在△BCE中,由余弦定理得BE2=x2-x+1;
$∠{B}_{1}{C}_{1}E=\frac{2π}{3}$,∴在△EB1C1中,由余弦定理得$E{{B}_{1}}^{2}$=1+(2-x)2+(2-x)=x2-5x+7;
在Rt△BB1E中,$B{E}^{2}+E{{B}_{1}}^{2}=B{{B}_{1}}^{2}$;
∴2x2-6x+8=4;
解得x=1,或x=2(舍去);
∴E为CC1中点时,EA⊥EB1;
(Ⅲ)由前面知AB⊥EB1,AE⊥EB1;
∴∠BAE等于二面角A-EB1-A1的大小;
AB⊥BB1C1C,∴AB⊥BE;
∴在Rt△ABE中$BE=1,AB=\sqrt{2}$,tan$∠BAE=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$;
∴二面角A-EB1-A1的正切值为$\frac{\sqrt{2}}{2}$.
点评 考查余弦定理,直角三角形边的关系,线面垂直的性质,线面垂直的判定定理,以及二面角平面角的概念及求法,正切函数的定义.


科目:高中数学 来源: 题型:解答题
 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40$\sqrt{2}$海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=$\frac{\sqrt{26}}{26}$,0°<θ<90°)且与点A相距10$\sqrt{13}$海里的位置C.
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40$\sqrt{2}$海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=$\frac{\sqrt{26}}{26}$,0°<θ<90°)且与点A相距10$\sqrt{13}$海里的位置C.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.4772 | B. | 0.1574 | C. | 0.2718 | D. | 0.1359 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<0或x≥2} | B. | {x|-1≤x≤0或x≥2} | C. | {x|-1≤x≤0或x>2} | D. | {x|0≤x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-1} | B. | {x|-1<x<3} | C. | {x|x>-2} | D. | {x|-2<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com