Question

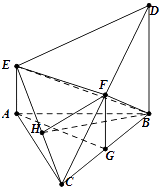
【题目】如图，在多面体ABCDE中，DB⊥平面ABC，AE∥DB，且△ABC是边长为2的等边三角形，2AE=BD=2．
（Ⅰ）若F是线段CD的中点，证明：EF⊥面DBC；
（Ⅱ）求二面角D﹣EC﹣B的平面角的余弦值．

Answer 1

【答案】证明：（Ⅰ）取BC的中点G，连接FG，AG，
∵AG⊥BC，AG⊥BD，BD∩BC=B，
∴AG⊥面DBC，
又∵AE∥BD∥FG，AE=FG，
∴AGFE为平行四边形，
∴EF∥AG，∴EF⊥面DBC．
解：（Ⅱ）连接BF，过F在面DEC内作EC的垂线，垂足为H
连接HB．∵EF⊥面DBC，∴BF⊥EF，
又∵BC=BD，∴BF⊥CD，∴BF⊥面EDC，
∴∠FHB为二面角D﹣EC﹣B的平面角，
在△DEC中，∵ ，∴ ，
在直角△BFH中， ， ， ，
∴cos∠FHB= = ．
∴二面角D﹣EC﹣B的平面角的余弦值为 ．

【解析】（Ⅰ）取BC的中点G，连接FG，AG，推导出AG⊥面DBC，AGFE为平行四边形，由此能证明EF⊥面DBC．（Ⅱ）连接BF，过F在面DEC内作EC的垂线，垂足为H，连接HB，则∠FHB为二面角D﹣EC﹣B的平面角，由此能求出二面角D﹣EC﹣B的平面角的余弦值．
【考点精析】掌握直线与平面垂直的判定是解答本题的根本，需要知道一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．