
分析 根据题意,利用同角三角函数的基本关系求得sin(x+$\frac{π}{4}$)、tan(x+$\frac{π}{4}$)的值,再利用两角和与差的三角公式、诱导公式,即可求出结果.
解答 解:∵$\frac{17π}{12}$<x<$\frac{7π}{4}$,∴x+$\frac{π}{4}$∈($\frac{5π}{3}$,2π),
又cos(x+$\frac{π}{4}$)=$\frac{3}{5}$,
∴sin(x+$\frac{π}{4}$)=-$\sqrt{1{-cos}^{2}(x+\frac{π}{4})}$=-$\frac{4}{5}$,
∴tan(x+$\frac{π}{4}$)=-$\frac{4}{3}$;
∴$\frac{sin2x+{2sin}^{2}x}{1-tanx}$=$\frac{sin2x(1+\frac{{2sin}^{2}x}{2sinxcosx})}{1-tanx}$
=sin2x•$\frac{1+tanx}{1-tanx}$
=-cos(2x+$\frac{π}{2}$)•$\frac{tan\frac{π}{4}+tanx}{1-tan\frac{π}{4}tanx}$
=-[2${cos}^{2}(x+\frac{π}{4})$-1]•tan(x+$\frac{π}{4}$)
=-[2×${(\frac{3}{5})}^{2}$-1]×(-$\frac{4}{3}$)
=-$\frac{28}{75}$.
点评 本题主要考查了同角三角函数的基本关系、两角和与差的三角公式的应用问题,是基础题目.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:选择题
| A. | a46 | B. | a89 | C. | a342 | D. | a387 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2cos$\frac{α}{2}$ | B. | -2cos$\frac{α}{2}$ | C. | 2sin$\frac{α}{2}$ | D. | -2sin$\frac{α}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
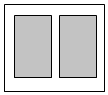 现需设计2016年春季湖北省重点高中联考协作体期中考试数学试卷,该试卷含有大小相等的左右相等两个矩形栏目(即图中阴影部分),这两栏的面积之和为720cm2,四周空白的宽度为4cm,两栏之间的中缝空白的宽度为2cm,设试卷的高和宽分别为xcm,ycm.
现需设计2016年春季湖北省重点高中联考协作体期中考试数学试卷,该试卷含有大小相等的左右相等两个矩形栏目(即图中阴影部分),这两栏的面积之和为720cm2,四周空白的宽度为4cm,两栏之间的中缝空白的宽度为2cm,设试卷的高和宽分别为xcm,ycm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com