
 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积是( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积是( )| A. | 36πcm2 | B. | 25πcm2 | C. | 16πcm2 | D. | 9πcm2 |
分析 首先由三视图还原几何体,得到其外接球半径,根据求的表面积公式求值.
解答 解:三视图表示的几何体为三棱锥D-ABC,且四个面为直角三角形;其中AD⊥平面ABC,底面ABC为等腰直角三角形,其斜边长为4,BC⊥平面ABD,取CD中点O,因为△ACD和△BCD为公用斜边CD的直角三角形,那么OA=$\frac{1}{2}$CD=OC=OD=OB,故三棱锥D-ABC的外接球心为O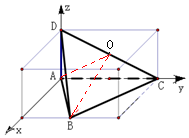
在Rt△DAC中,CD=$\sqrt{A{D}^{2}+A{C}^{2}}$=5,R2=($\frac{5}{2}$)2=$\frac{25}{4}$
则三棱锥外接球的表面积为4πR2=25πcm2;
故选B.
点评 本题考查了由几何体的三视图求几何体外接球表面积;关键是正确还原几何体,求出外接球的半径.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x≤2} | B. | {x|1≤x≤2} | C. | {x|x≤2且x≠1} | D. | {x|x≥0且x≠1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {1,3,5} | C. | {1,2,4} | D. | {3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 高一学生被抽到的概率最大 | B. | 高三学生被抽到的概率最大 | ||
| C. | 高三学生被抽到的概率最小 | D. | 每名学生被抽到的概率相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com