
【题目】如图,![]() 平面
平面![]() 分别是
分别是![]() 上的动点,且
上的动点,且![]() .
.
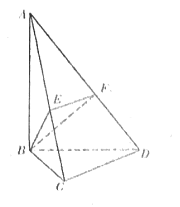
(1)若平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,求证:
,求证:![]() ;
;
(2)当平面![]() 平面
平面![]() 时,求平面
时,求平面![]() 与
与![]() 平面所成的二面角的余弦值.
平面所成的二面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)首先由线面平行的判定定理可得![]() 平面
平面![]() ,再由线面平行的性质定理即可得证;
,再由线面平行的性质定理即可得证;
(2)以点![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴,以过点
轴,以过点![]() 且垂直于
且垂直于![]() 的直线为
的直线为![]() 轴建立空间直角坐标系,利用空间向量法求出二面角的余弦值;
轴建立空间直角坐标系,利用空间向量法求出二面角的余弦值;
解:(1)由![]() ,
,![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
故![]() .
.
(2)因为![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() .
.
若平面![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() ,所以
,所以![]() ,
,
由![]() 且
且![]() ,
,
又![]() ,所以
,所以![]() .
.
以点![]() 为坐标原点,
为坐标原点,![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴,以过点
轴,以过点![]() 且垂直于
且垂直于![]() 的直线为
的直线为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
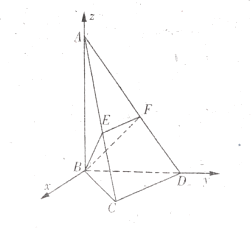
则![]() ,
,![]() ,设
,设![]()
则![]()
由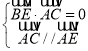 ,可得
,可得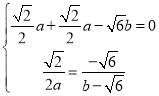 ,
,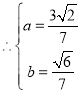 ,即
,即![]() ,所以可得
,所以可得![]() ,所以
,所以![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
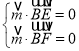 ,
,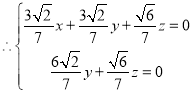 ,
,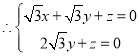 ,取
,取![]() ,得
,得![]()
所以![]()
易知平面![]() 的法向量为
的法向量为![]() ,
,
设平面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() ,
,
则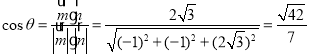 ,
,
结合图形可知平面![]() 与平面
与平面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】中国铁路总公司相关负责人表示,到2018年底,全国铁路营业里程达到13.1万公里,其中高铁营业里程2.9万公里,超过世界高铁总里程的三分之二,下图是2014年到2018年铁路和高铁运营里程(单位:万公里)的折线图,以下结论不正确的是( )

A.每相邻两年相比较,2014年到2015年铁路运营里程增加最显著
B.从2014年到2018年这5年,高铁运营里程与年价正相关
C.2018年高铁运营里程比2014年高铁运营里程增长80%以上
D.从2014年到2018年这5年,高铁运营里程数依次成等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() 是线段
是线段![]() 的中点,当
的中点,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设X~N(1,σ2),其正态分布密度曲线如图所示,且P(X≥3)=0.0228,那么向正方形OABC中随机投掷10000个点,则落入阴影部分的点的个数的估计值为( )
(附:随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
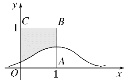
A. 6038 B. 6587 C. 7028 D. 7539
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,
,![]() 为平面内一动点,以线段
为平面内一动点,以线段![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)已知过坐标原点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 、
、![]() 两点,若在曲线
两点,若在曲线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,求
轴平行,求![]() ;
;
(2)已知![]() 在
在![]() 上的最大值不小于
上的最大值不小于![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)写出![]() 所有可能的零点个数及相应的
所有可能的零点个数及相应的![]() 的取值范围.(请直接写出结论)
的取值范围.(请直接写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com