Question

已知定义在[-2，2]上的奇函数f（x）满足：当x∈（0，2]时，f（x）=x（x-2）．
（1）求f（x）的解析式和值域；
（2）设g（x）=ln（x+2）-ax-2a，其中常数a＞0．
①试指出函数F（x）=g（f（x））的零点个数；
②若当1+

1

k

是函数F（x）=g（f（x））的一个零点时，相应的常数a记为a_k，其中k=1，2，…，n．
证明：a₁+a₂+…+a_n＜

7

6

（n∈N^*）．

Answer 1

考点：数列与函数的综合

专题：导数的综合应用,等差数列与等比数列

分析：（1）由奇函数性质得f（0）=0，当x∈[-2，0）时，f（x）=-f（-x）=-（-x）（-x-2）=-x（x+2），由此能求出f（x）的解析式和值域．
（2）①当t=0时，方程f（x）=t有三个实根，当t=1或t=-1时，方程f（x）=t只有一个实根，当t∈（0，1）或t∈（-1，0）时，方程f（x）=t有两个实根．设h（x）=

ln(x+2)

x+2

，x∈[-1，1]，h（-1）=0，h′(x)=

1-ln(x+2)

(x+2)2

，由此利用导数性质能求出函数F（x）=g（f（x））的零点个数．
②由已知得g（f（1+

1

k

））=0，g（f（1+

1

k

））=g（

1

k2

-1）=ln（

1

k2

+1-a_k（

1

k2

+1）=0，从而ak=

ln( 1 k2 +1)

1 k2 +1

，记m（x）=ln（x+1）-x，m′(x)=

1

x+1

-1=

-x

x+1

，由此利用导数性质能证明a₁+a₂+…+a_n＜

7

6

（n∈N^*）．

解答： （1）解：∵f（x）为奇函数，∴f（0）=0．
当x∈[-2，0）时，-x∈（0，2]，则f（x）=-f（-x）=-（-x）（-x-2）=-x（x+2），
∴f（x）=

x(x-2)，x∈[0，2] -x(x+2)，x∈[-2，0)

．
∵x∈[0，2]时，f（x）∈[-1，0]，x∈[-2，0），f（x）∈[0，1]，
∴f（x）的值域为[-1，1]．

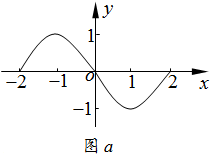
（2）①解：函数f（x）的图象如图a所示，当t=0时，方程f（x）=t有三个实根，
当t=1或t=-1时，方程f（x）=t只有一个实根，
当t∈（0，1）或t∈（-1，0）时，方程f（x）=t有两个实根．
由g（x）=0，解得a=

ln(x+2)

x+2

，
∵f（x）的值域为[-1，1]，
∴只需研究函数y=

ln(x+2)

x+2

在[-1，1]上的图象特征．
设h（x）=

ln(x+2)

x+2

，x∈[-1，1]，h（-1）=0，
h′(x)=

1-ln(x+2)

(x+2)2

，
令h′（x）=0，得x=e-2∈（0，1），h（e-2）=

1

e

．
∵当-1＜x＜e-2时，h′（x）＞0，当e-2＜x＜1时，h′（x）＜0，
又∵ln2³＜ln3²，即

ln2

2

＜

ln3

3

，
由h（0）=

ln2

2

，h（1）=

ln3

3

，得h（0）＜h（1），
∴h（x）的大致图象如图b所示．
根据图象b可知，当0＜a＜

ln2

2

、

ln2

2

＜a＜

ln3

3

、a=

1

e

时，
直线y=a与函数y=h（x）的图象仅有一个交点，
则函数g（x）在[-1，1]上仅有一个零点，记零点为t，
则t分别在区间（-1，0）、（0，1）上，根据图象a，
方程f（x）=t有两个交点，
因此函数F（x）=g（f（x））有两个零点．
类似地，当a=

ln2

2

时，函数g（x）在[-1，1]上仅有零点0，
因此函数F（x）有-1、0、1这三个零点．
当a=

ln3

3

时，函数g（x）在[-1，1]上有两个零点，一个零点是1，
另一个零点在（0，1）内，因此函数Y（x）有三个零点．
当

ln3

3

＜a＜

1

e

时，函数g（x）在[-1，1]上有两个零点，
且这两个零点均在（0，1）内，因此函数F（x）有四个零点．
当a＞

1

e

时，函数g（x）在[-1，1]上没有零点，因此函数F（x）没有零点．  
②证明：∵1+

1

k

是函数F（x）=g（f（x））的一个零点，
∴有g（f（1+

1

k

））=0，∵1+

1

k

∈（0，2），∴f（1+

1

k

）=

1

k2

-1，
∴g（f（1+

1

k

））=g（

1

k2

-1）=ln（

1

k2

+1-a_k（

1

k2

+1）=0，
∴ak=

ln( 1 k2 +1)

1 k2 +1

，k=1，2，…，n．
记m（x）=ln（x+1）-x，m′(x)=

1

x+1

-1=

-x

x+1

，
∵当x∈（0，1]时，m′（x）＜0，
∴当x∈（0，1]时，m（x）＜m（0）=0，即ln（x+1）＜x．
故有ln（

1

k2

+1）＜

1

k2

，则ak=

ln( 1 k2 +1)

1 k2 +1

＜

1 k2

1 k2 +1

=

1

k2+1

，k=1，2，…，n． 
当n=1时，a₁＜

1

2

＜

7

6

．
当n≥2时，∵

1

k2+1

＜

1

k2- 1 4

=

2

2k-1

-

2

2k+1

，
∴a₁+a₂+a₃+…+a_n＜

1

12+1

+

1

22+1

+

1

32+1

+…+

1

n2+1

＜

1

2

+(

2

3

-

2

5

)+(

2

5

-

2

7

)+…+(

2

2n-1

-

2

2n+1

)
=

1

2

+

2

3

-

2

2n+1

=

7

6

-

2

2n+1

＜

7

6

．
综上，有a₁+a₂+…+a_n＜

7

6

（n∈N^*）．

点评：本题主要考查函数的性质、分段函数、导数应用、一元二次方程的求解、连续函数的零点存在性定理，放缩法证明数列不等式，考查学生数形结合、分类讨论的数学思想，以及计算推理能力及分析问题、解决问题的能力及创新意识．