
分析 (1)由a-$\frac{1}{a}$=1,可得a-a-1=1.a2+a-2=(a-a-1)2+2,a+a-1=±$\sqrt{(a-{a}^{-1})^{2}+4}$,再利用乘法公式化简代入即可得出.
(2)对数的换底公式:logab=$\frac{lo{g}_{c}b}{lo{g}_{c}a}$(a,b,c>0,且a,c≠1).下面给出证明:设logab=x,化为指数式:ax=b>0,两边取以c为底的对数可得:xlogca=logcb,化简整理即可得出.
解答 (1)解:∵a-$\frac{1}{a}$=1,∴a-a-1=1.
a2+a-2=(a-a-1)2+2=3,
a+a-1=±$\sqrt{(a-{a}^{-1})^{2}+4}$=±$\sqrt{5}$.
∴$\frac{{({{a^3}+{a^{-3}}})({{a^2}+{a^{-2}}-3})}}{{{a^4}-{a^{-4}}}}$=$\frac{(a+{a}^{-1})({a}^{2}+{a}^{-2}-1)({a}^{2}+{a}^{-2}-3)}{(a+{a}^{-1})(a-{a}^{-1})({a}^{2}+{a}^{-2})}$=$\frac{(3-1)(3-3)}{1×3}$=0.
(2)对数的换底公式:logab=$\frac{lo{g}_{c}b}{lo{g}_{c}a}$(a,b,c>0,且a,c≠1).
证明:设logab=x,
化为指数式:ax=b>0,
两边取以c为底的对数可得:xlogca=logcb,
∵logca≠0,
化为x=$\frac{lo{g}_{c}b}{lo{g}_{c}a}$,即logab=$\frac{lo{g}_{c}b}{lo{g}_{c}a}$(a,b,c>0,且a,c≠1).
点评 本题考查了指数幂与对数的运算性质、对数的换底公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
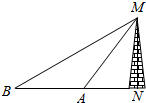 如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )
如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )| A. | 100$\sqrt{2}$m | B. | 100$\sqrt{3}$m | C. | 100m | D. | 200m |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | $\frac{16}{3}$ | C. | $\frac{256}{9}$ | D. | $\frac{128}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com