
����Ŀ��һֻҩ������IJ�����![]() ��һ����Χ�����¶�
��һ����Χ�����¶�![]() �й�, ���ռ��˸���ҩ�������6��۲��������±���
�й�, ���ռ��˸���ҩ�������6��۲��������±���
�¶� | 21 | 23 | 24 | 27 | 29 | 32 |
������ | 6 | 11 | 20 | 27 | 57 | 77 |
(1)�������Իع�ģ�ͣ���![]() ����
����![]() �Ļع鷽��
�Ļع鷽��![]() =
=![]() x+
x+![]() ����ȷ��0.1����
����ȷ��0.1����
(2)���÷����Իع�ģ����![]() ��
��![]() �Ļع鷽��Ϊ
�Ļع鷽��Ϊ![]()
![]() �����ָ��
�����ָ��![]()
( i )���� (1)�е����Իع�ģ����ȣ���![]() ˵������ģ�͵����Ч������.
˵������ģ�͵����Ч������.
( ii )�����Ч���õ�ģ��Ԥ���¶�Ϊ![]() ʱ����ҩ������IJ����������ȡ������.
ʱ����ҩ������IJ����������ȡ������.
����һ������(x1,y1), (x2,y2), ...,(xn,yn), ��ع�ֱ��![]() =
=![]() x+
x+![]() ��б�ʺͽؾ����С���˹���Ϊ
��б�ʺͽؾ����С���˹���Ϊ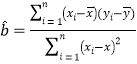 ��
��![]() �����ָ��
�����ָ��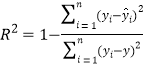 ��
��
![]()
![]()
![]()
![]() ��
��
���𰸡���1��![]() =6.6x138.6����2���ع鷽��
=6.6x138.6����2���ع鷽��![]() �����Իع鷽��
�����Իع鷽��![]() =6.6x138.6���Ч�����ã�190��
=6.6x138.6���Ч�����ã�190��
����������������1�������⼰�����Ĺ�ʽ�Ͳο����ݿ����![]() ��
��![]() �������ɵ����Իع鷽������2��( i )����������(1)�е����Իع�ģ�͵����ָ��
�������ɵ����Իع鷽������2��( i )����������(1)�е����Իع�ģ�͵����ָ��![]() ���ʿɵûع鷽��
���ʿɵûع鷽��![]() �����Իع鷽��
�����Իع鷽��![]() =6.6x138.6���Ч��������( ii )��x=35����
=6.6x138.6���Ч��������( ii )��x=35����![]() �ɵù���ֵ��
�ɵù���ֵ��
��⣺(1)�������![]() ��
�� ![]() ��
��
![]() ��
��![]() ��
��
���� ,
,
��![]() 336.6
336.6![]() 26=138.6��
26=138.6��
��y����x�����Իع鷽��Ϊ![]() =6.6x138.6��
=6.6x138.6��
(2) ( i )������������õ����Իع鷽��Ϊ![]() =6.6x138.6��
=6.6x138.6��
��![]() ��
��
�ʵ����ָ��Ϊ ��
��
��Ϊ0.9398��0.9522��
���Իع鷽��![]() �����Իع鷽��
�����Իع鷽��![]() =6.6x138.6���Ч�����ã�
=6.6x138.6���Ч�����ã�
( ii )��( i )�õ�x=![]() Cʱ��
Cʱ��![]() ��
��
�����¶�x=35��ʱ������ҩ������IJ���������Ϊ190����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ���Ǽ���������
���Ǽ���������![]() ����������
����������![]() ������
������![]() �������������ʣ�
�������������ʣ�
![]() ��
��![]() ��
��![]() ʱ����
ʱ����![]() �ĵ�����������
�ĵ�����������![]() ֻ���ж��������䣬����Ҫ֤��
ֻ���ж��������䣬����Ҫ֤��![]() ��
��
![]() ��
��![]() ��
��![]() ������
������![]() �����ֵΪ
�����ֵΪ![]() ����
����![]() �Ľ���ʽ��
�Ľ���ʽ��
![]() ��
��![]() ������
������![]() ǡ���Ľ⣬��ʵ��a��ȡֵ��Χ��
ǡ���Ľ⣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ĸ�С���ﻻ��λ����ʼ����á�è�ֱ����� 1��2��3��4 ��λ���ϣ���ͼ���� ��һ��ǰ���Ŷ��ﻥ����λ���ڶ��������ж��ﻥ����λ,.....,�������������ȥ����ô�� 2013 �λ�����λ��С�õ���λ��Ӧ����( )

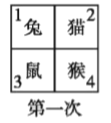
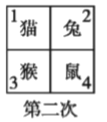
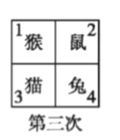
A. ��� 1 B. ��� 2 C. ��� 3 D. ��� 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=Asin����x+�գ�+1��A��0���أ�0��|��|�� ![]() ����ͼ������һ����͵���P����
����ͼ������һ����͵���P���� ![]() ����1��������f��x1��=1��f��x2��=3��|x1��x2|����СֵΪ
����1��������f��x1��=1��f��x2��=3��|x1��x2|����СֵΪ ![]() �� ������f����+
�� ������f����+ ![]() ��=
��= ![]() ���Ҧ�Ϊ�������Ľǣ���sin��+cos����ֵ��
���Ҧ�Ϊ�������Ľǣ���sin��+cos����ֵ��
��������y=f��x��+m������[0�� ![]() ]�����������
]�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l��x+2y-2=0������
��1����P��-2��-1������ֱ��l�ĶԳƵ����ꣻ
��2��ֱ��l���ڵ㣨1��1���ԳƵ�ֱ�߷��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����
����![]() ��ԭ�㴦������Ϊ
��ԭ�㴦������Ϊ![]() .
.
��1��֤��������![]() ��
��![]() ���������н��㣻
���������н��㣻
��2��������![]() ��
��![]() ��������Ľ���Ϊ
��������Ľ���Ϊ![]() �������ڵ�
�������ڵ�![]() ��������Ϊֱ��
��������Ϊֱ��![]() ����֤������
����֤������![]() �ϵĵ㶼����ֱ��
�ϵĵ㶼����ֱ��![]() ���Ϸ� ��
���Ϸ� ��
��3��������![]() �ķ���
�ķ���![]() ��
��![]() Ϊ��ʵ�����в���ʵ��
Ϊ��ʵ�����в���ʵ��![]() ��֤��
��֤��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��Բ�ĵ���뾶Ϊ1����Ϊ3����Բ����һ���뾶Ϊx���ڽ�Բ��.

(1)����x��ʾԲ���ĸߣ�
(2)��xΪ��ֵʱ��Բ���IJ���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ݵ��飬ij������300����´�ͳũҵ��ũ���˾�������6000Ԫ��Ϊ������ũ������룬�����������������ʱ����������ּӹ���ҵ���Ե��ص�ũ��Ʒ������ӹ���ͬʱ���յ��ز���ũ�����ӹ���ҵ�������ݹ��ƣ������![]() ���˽���ҵ��������ôʣ�´��´�ͳũҵ��ũ����˾��������������
���˽���ҵ��������ôʣ�´��´�ͳũҵ��ũ����˾��������������![]() ����������ҵ������ũ����˾�������Ϊ
����������ҵ������ũ����˾�������Ϊ![]() Ԫ��
Ԫ��
��1���ڽ����ӹ���ҵ����ũ�������ҵ�������ܹ�ʹʣ�´��´�ͳũҵũ������������������ֵ��
��2��Ϊ�˱�֤��ͳũҵ��˳�����У�����ũ�����ӹ���ҵ���������ܳ�����������![]() �����������������ũ��
�����������������ũ��![]() ȡ��ֵʱ����ʹ300��ũ��������������
ȡ��ֵʱ����ʹ300��ũ��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У���![]() ��һ����Ҫ������
��һ����Ҫ������![]() �����Ĺ������ȣ�
�����Ĺ������ȣ�
�����ö����Լ��������������������![]() ��
��![]() �Ƿ��й�ϵ�����������
�Ƿ��й�ϵ�����������![]() �Ĺ۲�ֵ
�Ĺ۲�ֵ![]() ֵԽ��
ֵԽ��![]() ��
��![]() �й�ϵ�������Ŀ�����Խ��
�й�ϵ�������Ŀ�����Խ��
���ڻع����ģ���У������ָ��Խ����в�ƽ����ԽС��ģ�͵����Ч��Խ�ã�
����![]() ��
��![]() ��������ȵ�ʵ������
��������ȵ�ʵ������![]() �Ǵ�������
�Ǵ�������
��ijУ��������![]() ���࣬
���࣬![]() ����
����![]() �ˣ�
�ˣ�![]() ����
����![]() �ˣ�
�ˣ�![]() ����
����![]() �ˣ��ɴ��Ʋ�������
�ˣ��ɴ��Ʋ�������![]() �ˣ����������������������.
�ˣ����������������������.
��������������Ϊ__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com