
分析 (1)根据极坐标以及直角坐标方程的关系求出圆C的直角坐标方程即可,联立直线的参数方程和圆的方程,求出弦长即可;
(2)求出直线的普通方程以及圆的参数方程,可设曲线C上的动点P(2+2cosθ,2sinθ),求出点P到直线l的距离,结合三角函数的性质求出△ABP的面积的最大值.
解答 解:(1)由ρ=4cosθ得ρ2=4ρcosθ,
所以x2+y2-4x=0,所以圆C的直角坐标方程为(x-2)2+y2=4.
将直线l的参数方程代入圆C:(x-2)2+y2=4,并整理得${t^2}+2\sqrt{2}t=0$,
解得t1=0,${t_2}=-2\sqrt{2}$.
所以直线l被圆C截得的弦长为$|{t_1}-{t_2}|=2\sqrt{2}$.
(2)直线l的普通方程为x-y-4=0.
圆C的参数方程为$\left\{{\begin{array}{l}{x=2+2cosθ}\\{y=2sinθ}\end{array}}\right.$(θ为参数),
可设曲线C上的动点P(2+2cosθ,2sinθ),
则点P到直线l的距离$d=\frac{|2+2cosθ-2sinθ-4|}{{\sqrt{2}}}$=$|2cos(θ+\frac{π}{4})-\sqrt{2}|$,
当$cos(θ+\frac{π}{4})=-1$时,d取最大值,且d的最大值为$2+\sqrt{2}$.
所以${S_{△ABP}}≤\frac{1}{2}×2\sqrt{2}×(2+\sqrt{2})=2+2\sqrt{2}$,
即△ABP的面积的最大值为$2+\sqrt{2}$.
点评 本题考查了极坐标方程以及普通方程的转化,考查点到直线的距离以及三角函数的性质,是一道中档题.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 512 | B. | 511 | C. | 1024 | D. | 1023 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x4+2x | B. | y=2|x| | C. | y=2x-2-x | D. | $y={log_{\frac{1}{2}}}|x|-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | 1 | C. | $-\frac{3}{5}$ | D. | $-\frac{7}{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?p | B. | q | C. | p∨(?q) | D. | (?p)∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
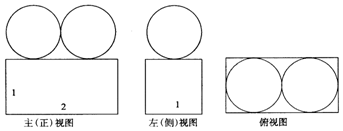
| A. | 2+$\frac{4π}{3}$ | B. | 2+$\frac{π}{3}$ | C. | 1+$\frac{4π}{3}$ | D. | 10+8π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com