
���� ��1�����õȿ������¼����ʼ��㹫ʽ�����ijѧ�����鵽�ĸ��ʣ��ɴ����÷ֲ����������������ɷ�С��������������Ů����������
��2������������¼������������ѡ����2��ѧ����ǡ��1��Ů�������Ļ����¼��������ɴ������ѡ����2��ѧ����ǡ��1��Ů���ĸ��ʣ�
��� �⣺��1��ij��ѧ����ϵ������45����Ů��15����
���շֲ�����ķ����齨��һ��4�˵���»�ɷ�С�飮
��ijѧ�����鵽�ĸ���p=$\frac{4}{45+15}$=$\frac{1}{15}$��
�ɷ�С������������Ϊ��45��$\frac{1}{15}$=3��
Ů��������Ϊ��15��$\frac{1}{15}$=1��
��2������ɷ�С�����ѡ��2��ѧ�������������༭���������ȴ�С����ѡ��1��ѧ������Ϣ���࣬
��ѧ�������������ٴ�С����ʣ�µ�ѧ����ѡ1�������ڼ�����
�����¼�����n=4��3=12��
ѡ����2��ѧ����ǡ��1��Ů�������Ļ����¼�����m=1��3+3��1=6��
��ѡ����2��ѧ����ǡ��1��Ů���ĸ���p=$\frac{m}{n}$=$\frac{6}{12}=\frac{1}{2}$��
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע��ֲ���������ʺ͵ȿ����¼����ʼ��㹫ʽ�ĺ������ã�


 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{5}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 3 | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
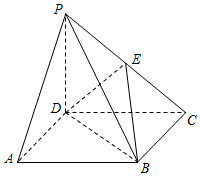 ������P-ABCD�У�����ABCD�������Σ�����PD��ֱ�ڵ���ABCD��PD=DC����E��PC���е㣮
������P-ABCD�У�����ABCD�������Σ�����PD��ֱ�ڵ���ABCD��PD=DC����E��PC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com