
分析 由题意求出C点的轨迹是以原点为圆心,以$\sqrt{8+{t}^{2}}$为半径的圆,再由点C到直线l:3x-4y+24=0的最小距离为$\frac{9}{5}$,转化为关于t的方程求解.
解答 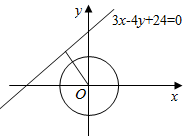 解:设C(x0,y0),∵A(-t,0),B(t,0),$\overrightarrow{AC}$•$\overrightarrow{BC}$=8,
解:设C(x0,y0),∵A(-t,0),B(t,0),$\overrightarrow{AC}$•$\overrightarrow{BC}$=8,
∴(x0+t,y0)•(x0-t,y0)=8,即${{x}_{0}}^{2}-{t}^{2}+{{y}_{0}}^{2}=8$,
∴${{x}_{0}}^{2}+{{y}_{0}}^{2}=8+{t}^{2}$,则点C在以原点为圆心,以$\sqrt{8+{t}^{2}}$为半径的圆上,
又点C到直线l:3x-4y+24=0的最小距离为$\frac{9}{5}$,
即$\frac{|24|}{\sqrt{{3}^{2}+(-4)^{2}}}-\sqrt{8+{t}^{2}}=\frac{9}{5}$,
∴$\sqrt{8+{t}^{2}}=3$,解得:t=±1,
∵t>0,∴t=1.
故答案为:1.
点评 本题考查平面向量的数量积运算,考查了直线与圆位置关系的应用,训练了点到直线距离公式的应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
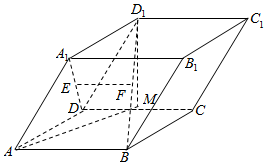 如图,在平行六面体ABCD-A1B1C1D1中,侧面DCC1D1是菱形,且平面DCC1D1⊥平面ABCD,∠D1DC=$\frac{π}{3}$,E是A1D的中点,F是BD1的中点.
如图,在平行六面体ABCD-A1B1C1D1中,侧面DCC1D1是菱形,且平面DCC1D1⊥平面ABCD,∠D1DC=$\frac{π}{3}$,E是A1D的中点,F是BD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com