
| A. | (1,2) | B. | (1,3) | C. | (2,+∞) | D. | (3,+∞) |
分析 设三角形的三边从小到大依次为a,b,c,因为锐角△ABC三内角A、B、C的度数成等差数列得到B为60°,然后利用余弦定理表示出cosB得到一个关系式,根据三角形为锐角三角形得到a2+b2-c2>0,把求得的关系式代入不等式即可求得最大边c与最小边a比值即m的范围.
解答 解:设三角形的三边从小到大依次为a,b,c,
因为三内角的度数成等差数列,所以2B=A+C,则A+B+C=3B=180°
故可得B=60°,根据余弦定理得:cosB=cos60°=$\frac{1}{2}$=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,于是b2=a2+c2-ac,
又因为△ABC为锐角三角形,故a2+b2-c2>0,
于是2a2-ac>0,即$\frac{c}{a}$<2,
∵c>a,即:$\frac{c}{a}$>1,
则m=$\frac{c}{a}$∈(1,2).
故选:A.
点评 此题考查学生掌握等差数列的性质及钝角三角形三边的平方关系,灵活运用余弦定理化简求值,是一道中档题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
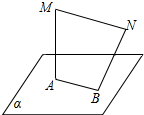 如图,MA⊥平面α,AB?平面α,BN与平面α所成的角为60°,且AB⊥BN,MA=AB=BN=1,则MN的长为( )
如图,MA⊥平面α,AB?平面α,BN与平面α所成的角为60°,且AB⊥BN,MA=AB=BN=1,则MN的长为( )| A. | $\sqrt{3+\sqrt{3}}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3-\sqrt{3}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{a}$)xlna | B. | -a-xlna | C. | a-xlna | D. | axln$\frac{1}{a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com