
分析 (1)利用和的余弦、正弦公式,结合三角不等式,即可证明结论;
(2)由(1)可得|cos[α+(β+γ]=|cosα|+|sin(β+γ)|≤|cosα|+|cosβ|+|cosγ|,即可证明结论.
解答 证明:(1)|cos(α+β)|=|cosαcosβ-sinαsinβ|≤|cosαcosβ|+|sinαsinβ|≤|cosα|+|sinβ|;
|sin(α+β)|=|sinαcosβ-cosαsinβ|≤|sinαcosβ|+|cosαsinβ|≤|cosα|+|cosβ|.
(2)由(1)可得|cos[α+(β+γ)]≤|cosα|+|sin(β+γ)|≤|cosα|+|cosβ|+|cosγ|,
∵α+β+γ=0,
∴|cos[α+β+γ]=1
∴|cosα|+|cosβ|+|cosγ|≥1.
点评 本题考查和的余弦、正弦公式,考查绝对值三角不等式,考查学生分析解决问题的能力,正确运用绝对值三角不等式是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
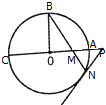 如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线交CA的延长线于P.
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线交CA的延长线于P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图正方形BCDE的边长为a,已知AB=$\sqrt{3}$BC,将△ABE 沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:
如图正方形BCDE的边长为a,已知AB=$\sqrt{3}$BC,将△ABE 沿BE边折起,折起后A点在平面BCDE上的射影为D点,则翻折后的几何体中有如下描述:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com