
【题目】在平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() 右焦点的直线
右焦点的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,且直线
的中点,且直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设另一直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,原点
两点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由题意,焦点![]() ,所以
,所以![]() ,再由
,再由![]() ,得
,得![]() ,
,
进而得![]() ,即可得到椭圆的标准方程.
,即可得到椭圆的标准方程.
(Ⅱ)由题意,①当直线![]() 的斜率不存在时或者斜率为0时,易得
的斜率不存在时或者斜率为0时,易得![]() ;
;
②设直线![]() 的方程为:
的方程为: ![]() ,由题意,原点
,由题意,原点![]() 到直线
到直线![]() 的距离得到
的距离得到![]() .
.
设交点![]() 的坐标分别为
的坐标分别为![]() ,联立方程组,得到
,联立方程组,得到![]() ,再由弦长公式,利用均值不等式,即可求解最值,进而得到面积的最值.
,再由弦长公式,利用均值不等式,即可求解最值,进而得到面积的最值.
试题解析:
(Ⅰ)由题意,直线![]() 与
与![]() 轴交于焦点:
轴交于焦点: ![]() ,
, ![]() ,设
,设![]() ,
, ![]() ,
, ![]() ,则:
,则: ![]() ,
,
![]() ,
, ![]()
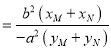
![]() ,
,
![]() ,又
,又![]() ,
, ![]()
![]() ,
,
即椭圆![]() 的方程为:
的方程为: ![]()
(Ⅱ)由题意,①当直线![]() 的斜率不存在时或者斜率为0时,易得
的斜率不存在时或者斜率为0时,易得![]() ;
;
②当直线![]() 的斜率存在时且不为0时,设直线
的斜率存在时且不为0时,设直线![]() 的方程为:
的方程为: ![]() ,由题意,原点
,由题意,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,故
,故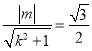 ,
,
![]() .设交点
.设交点![]() 的坐标分别为:
的坐标分别为: ![]() ,
, ![]() ,
,
则: 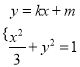 ,
, ![]() ,
,
由题意![]() ,
, ![]()
![]() .
.
![]()
![]()
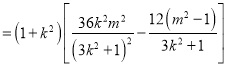
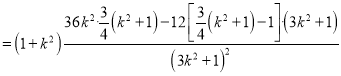
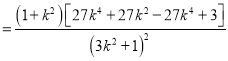
![]()
![]()
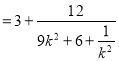
![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立, ![]() ;
;
综上所述,当直线![]() 的斜率
的斜率![]() 时,
时,
即![]() 时,
时, ![]() 面积的最大值
面积的最大值
![]()
![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a4x﹣a2x+1+1﹣b(a>0)在区间[1,2]上有最大值9和最小值1
(1)求a,b的值;
(2)若不等式f(x)﹣k4x≥0在x∈[﹣1,1]上有解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣3x﹣4≤0},B={x|x2﹣2mx+m2﹣9≤0},C={y|y=2x+b,x∈R}
(1)若A∩B=[0,4],求实数m的值;
(2)若A∩C=,求实数b的取值范围;
(3)若A∪B=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣a是奇函数
﹣a是奇函数
(1)求实数a的值;
(2)判断函数在R上的单调性并用函数单调性的定义证明;
(3)对任意的实数x,不等式f(x)<m﹣1恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=x2+bx+c满足f(2)=f(﹣2),且函数的f(x)的一个零点为1. (Ⅰ)求函数f(x)的解析式;
(Ⅱ)对任意的 ![]() ,4m2f(x)+f(x﹣1)≥4﹣4m2恒成立,求实数m的取值范围.
,4m2f(x)+f(x﹣1)≥4﹣4m2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为:
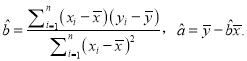
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() 的极坐标方程为
的极坐标方程为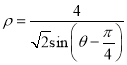 .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 为曲线
为曲线![]() 上任意一点,
上任意一点, ![]() 为直线
为直线![]() 任意一点,求
任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com