练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，以为极点， 轴的正半轴为极轴建立极坐标系，曲线的参数方程为（为参数， ），直线的极坐标方程为.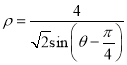

    （1）写出曲线的普通方程和直线的直角坐标方程；

    （2）为曲线上任意一点， 为直线任意一点，求的最小值.

    【答案】（1）； ；（2）.

    【解析】试题分析：（1）曲线消去可得普通方程，注意参数的范围，利用极直互化可得直线的直角坐标方程；

    （2）圆上的点到直线的距离可以转化为圆心到直线的距离求解.

    试题解析：

    （1）曲线的参数方程为，（ 为参数， ），

    消去参数，可得，

    由于，∴，

    故曲线的轨迹方程是上半圆.

    ∵直线，即，即，

    故直线的直角坐标方程为.

    （2）由题意可得点在直线上，点在半圆上，半圆的圆心到直线的距离等于，即的最小值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，过椭圆右焦点的直线交椭圆于两点， 为的中点，且直线的斜率为．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）设另一直线与椭圆交于两点，原点到直线的距离为，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且

    （1）求证：不论为何值，总有平面BEF⊥平面ABC；

    （2）当λ为何值时，平面BEF⊥平面ACD ?

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ，设b＞a≥0，若f（a）=f（b），则af（b）的取值范围是（ ）
    A.[ ，2）
    B.[﹣ ，+∞）
    C.[﹣ ，﹣ ）
    D.[﹣ ， ]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f（x）=x2+bx+c，当x∈R时f（x）=f（2﹣x）恒成立，且3是f（x）的一个零点． （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）设g（x）=f（ax）（a＞1），若函数g（x）在区间[﹣1，1]上的最大值等于5，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（其中，且为常数）.

    （1）当时，求函数的单调区间；

    （2）若对于任意的，都有成立，求的取值范围；

    （3）若方程在上有且只有一个实根，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在对人们的休闲方式的一次调查中，共调查了124人，其中女性70人，男性54人.女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动.

    （1）根据以上数据建立一个列联表；

    （2）判断性别与休闲方式是否有关系.

    0.05

    0.025

    0.010

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是一个几何体的正视图和俯视图．

    (Ⅰ)试判断该几何体是什么几何体？

    (Ⅱ)画出其侧视图，并求该平面图形的面积；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义：在等式 中，把， ， ，…， 叫做三项式的次系数列(如三项式的1次系数列是1，1，1).

    (1)填空：三项式的2次系数列是_______________；

    三项式的3次系数列是_______________；

    (2)由杨辉三角数阵表可以得到二项式系数的性质,类似的请用三项式次系数列中的系数表示 (无须证明)；

    (3)求的值.

    查看答案和解析>>

    同步练习册答案