
【题目】在某城市街道上一侧路边边缘![]() 某处安装路灯,路宽
某处安装路灯,路宽![]() 为
为![]() 米,灯杆
米,灯杆![]() 长4米,且与灯柱
长4米,且与灯柱![]() 成
成![]() 角,路灯采用可旋转灯口方向的锥形灯罩,灯罩轴线
角,路灯采用可旋转灯口方向的锥形灯罩,灯罩轴线![]() 与灯的边缘光线(如图
与灯的边缘光线(如图![]() ,
, ![]() )都成
)都成![]() 角,当灯罩轴线
角,当灯罩轴线![]() 与灯杆
与灯杆![]() 垂直时,灯罩轴线正好通过
垂直时,灯罩轴线正好通过![]() 的中点.
的中点.
(I)求灯柱![]() 的高
的高![]() 为多少米;
为多少米;
(II)设![]() ,且
,且![]() ,求灯所照射路面宽度
,求灯所照射路面宽度![]() 的最小值.
的最小值.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的![]() .现有3名工人独立地从中任选一个项目参与建设.
.现有3名工人独立地从中任选一个项目参与建设.
(1)求他们选择的项目所属类别互不相同的概率;
(2)记ξ为3人中选择的项目属于基础设施工程或产业建设工程的人数,求ξ的分布列及均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 满足
满足![]() ,其中
,其中![]() ,且
,且![]() ,
, ![]() 为常数.
为常数.
(1)若![]() 是等差数列,且公差
是等差数列,且公差![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且存在
,且存在![]() ,使得
,使得![]() 对任意的
对任意的![]() 都成立,求
都成立,求![]() 的最小值;
的最小值;
(3)若![]() ,且数列
,且数列![]() 不是常数列,如果存在正整数
不是常数列,如果存在正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 均成立. 求所有满足条件的数列
均成立. 求所有满足条件的数列![]() 中
中![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A, B, C的对边分别为a, b, c,且![]() .
.
(Ⅰ)求角C的大小;
(Ⅱ)设角A的平分线交BC于D,且AD=![]() ,若b=
,若b=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,圆
,圆![]() ,以动点
,以动点![]() 为圆心的圆经过点
为圆心的圆经过点![]() ,且圆
,且圆![]() 与圆
与圆![]() 内切.
内切.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 轴平分
轴平分![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料溶化完毕时钢水的含碳量x与冶炼时间y(从炉料溶化完毕到出钢的时间)的一组数据,如表所示:
x(0.01%) | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程.
(3)预报当钢水含碳量为160个0.01%时,应冶炼多少分钟?
参考公式:r=![]()
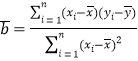 ,
,
线性回归方程![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com