
分析 作出图象,由题意可得S=$\frac{1}{2}$=$\frac{{h}_{2}}{sinα}$$\frac{{h}_{1}}{sin(90°-α)}$,由三角函数的最值可得.
解答 解:如图AB=$\frac{{h}_{2}}{sinα}$,AC=$\frac{{h}_{1}}{sin(90°-α)}$,
∴△ABC面积S=$\frac{1}{2}$=$\frac{{h}_{2}}{sinα}$$\frac{{h}_{1}}{sin(90°-α)}$
=$\frac{{h}_{1}{h}_{2}}{2sinαcosα}$=$\frac{{h}_{1}{h}_{2}}{sin2α}$
当sin2α取最大值1即2α=90°即α=45°时,
△ABC面积取最小值为h1h2.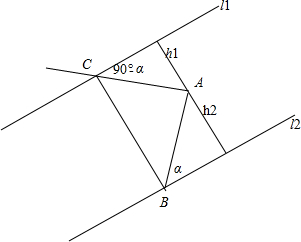
点评 本题考查直线的一般式方程和平行关系,涉及三角函数求最值,属中档题.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
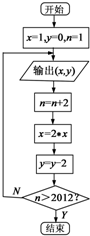 某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )
某程序框图如图所示,现将输出(x,y)值依次记为:(x1,y1),(x2,y2),…,(xn,yn)…若程序运行中输出的一个数组是(x,-10)则数组中的x=( )| A. | 32 | B. | 24 | C. | 18 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 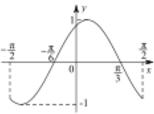 | B. | 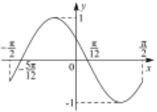 | ||
| C. | 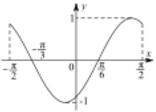 | D. | 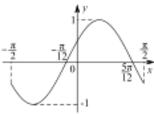 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com