
【题目】函数![]() 的一部分图象如图所示,其中
的一部分图象如图所示,其中![]() ,
,![]() ,
,![]() .
.

(1)求函数![]() 解析式;
解析式;
(2)求![]() 时,函数
时,函数![]() 的值域;
的值域;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求函数
的图象,求函数![]() 的单调递减区间.
的单调递减区间.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(本题16分)某乡镇为了进行美丽乡村建设,规划在长为10千米的河流OC的一侧建一条观光带,观光带的前一部分为曲线段OAB,设曲线段OAB为函数![]() ,
,![]() (单位:千米)的图象,且曲线段的顶点为
(单位:千米)的图象,且曲线段的顶点为![]() ;观光带的后一部分为线段BC,如图所示.
;观光带的后一部分为线段BC,如图所示.
(1)求曲线段OABC对应的函数![]() 的解析式;
的解析式;
(2)若计划在河流OC和观光带OABC之间新建一个如图所示的矩形绿化带MNPQ,绿化带由线段MQ,QP, PN构成,其中点P在线段BC上.当OM长为多少时,绿化带的总长度最长?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂品牌服装的年固定成本100万元,每生产1万件需另投入27万元,设服装厂一年内共生产该品牌服装![]() 万件并全部销售完,每万件的销售收入为R(
万件并全部销售完,每万件的销售收入为R(![]() )万元.且
)万元.且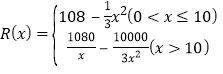
(1)写出年利润y(万元)关于年产量![]() (万件)的函数关系式;
(万件)的函数关系式;
(2)年产量为多少万件时,服装厂在这一品牌的生产中所获年利润最大?(注:年利润=年销售收入-年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.

(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中随机抽取部分高一学生调查其上学路上所需时间频(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() .
.

(1)求直方图中![]() 的值;
的值;
(2)如果上学路上所需时间不少于1小时的学生可申请在学校住宿,若招生 1200名请估计新生中有多少名学生可以申请住宿;
(3)从学校的高一学生中任选4名学生,这4名学生中上学路上所需时间少于 40分钟的人数记为![]() ,求
,求![]() 的分布列和数学期望.(以直方图中的频率作为概率).
的分布列和数学期望.(以直方图中的频率作为概率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的四棱锥![]() 中,底面
中,底面![]() 与侧面
与侧面![]() 垂直,且四边形
垂直,且四边形![]() 为正方形,
为正方形, ![]() ,点
,点![]() 为边
为边![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,且
上,且![]() ,过
,过![]() ,
, ![]() ,
, ![]() 三点的截面与平面
三点的截面与平面![]() 的交线为
的交线为![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成的角为( )
所成的角为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为保证学生夜晚安全,实行教师值夜班制度,已知![]() 共5名教师每周一到周五都要值一次夜班,每周如此,且没有两人同时值夜班,周六和周日不值夜班,若
共5名教师每周一到周五都要值一次夜班,每周如此,且没有两人同时值夜班,周六和周日不值夜班,若![]() 昨天值夜班,从今天起
昨天值夜班,从今天起![]() 至少连续4天不值夜班,
至少连续4天不值夜班, ![]() 周四值夜班,则今天是周___________.
周四值夜班,则今天是周___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com