Question

14．已知函数y=f（x）恒满足f（x+2）=f（x），且当x∈[-1，1]时，f（x）=2^|x|-1，则函数g（x）=f（x）-|lgx|在R上的零点的个数是8．

Answer 1

分析 作出f（x）与y=|lgx|的函数图象，根据函数图象的交点个数得出答案．

解答 解：∵f（x+2）=f（x），∴f（x）的周期为2，
令g（x）=0得f（x）=|lgx|，
作出y=f（x）与y=|lgx|的函数图象如图所示：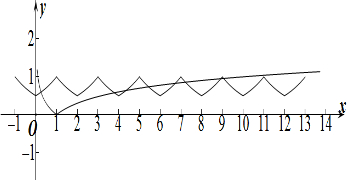

由图象可知f（x）与y=|lgx|在（0，1）上必有1解，
又f（x）的最小值为$\frac{1}{2}$，f（x）的最大值为1，
∵lg2＜lg$\sqrt{10}$=$\frac{1}{2}$，lg4＞lg$\sqrt{10}$=$\frac{1}{2}$，lg9＜1，lg11＞1，
∴f（x）与y=|lgx|在（10，+∞）上没有交点，
结合图象可知f（x）与y=|lgx|共有8个交点，
∴g（x）共有8个零点．
故答案为：8．

点评 本题考查了函数零点与图象的关系，属于中档题．