Question

1．已知底面为边长为2的正方形，侧棱长为1的直四棱柱ABCD-A₁B₁C₁D₁中，P，Q是面A₁B₁C₁D₁上的两个不同的动点．给出以下四个结论：
①若DP=$\sqrt{3}$，则DP在该四棱柱六个面上的投影长度之和的最大值为6$\sqrt{2}$；
②若P在面对角线A₁C₁上，则在棱DD₁上存在一点M使得MB₁⊥BP；
③若P，Q均在面对角线A₁C₁上，且PQ=1，则四面体BDPQ的体积一定是定值；
④若P，Q均在面对角线A₁C₁上，则四面体BDPQ在底面ABCD-A₁B₁C₁D₁上的投影恒为凸四边形的充要条件是PQ＞$\sqrt{2}$；
以上各结论中，正确结论的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 ①若DP=$\sqrt{3}$，P点落在以D₁为圆心，以$\sqrt{2}$为半径的弧上，求出DP在该四棱柱六个面上的投影长度之和的最大值，可判断①；
②三垂线定理可得：当OB与MB₁垂直时，MB₁⊥BP，判断M点是否在棱DD₁上，可判断②；
③若P，Q均在面对角线A₁C₁上，求出四面体BDPQ的体积，可判断③；
④根据充要性的条件，判断四面体BDPQ在底面ABCD-A₁B₁C₁D₁上的投影恒为凸四边形与PQ＞$\sqrt{2}$的关系，可判断④．

解答 解：若DP=$\sqrt{3}$，P点落在以D₁为圆心，以$\sqrt{2}$为半径的弧上，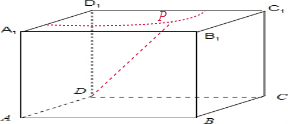

当P为弧的中点时，DP在该四棱柱六个面上的投影的和取最大值
此时DP在该四棱柱六个面上的投影均为$\sqrt{2}$，
故DP在该四棱柱六个面上的投影长度之和的最大值为6$\sqrt{2}$，故①正确；
若P在面对角线A₁C₁上，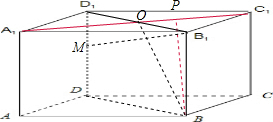

由三垂线定理可得：当OB与MB₁垂直时，MB₁⊥BP，
而当MB₁⊥BP时，D₁M=4＞1，
即棱DD₁上不存在一点M使得MB₁⊥BP，故②错误；
③若P，Q均在面对角线A₁C₁上，且PQ=1，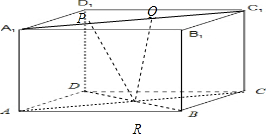

则△PQR的面积为定值$\frac{1}{2}$，且BD⊥平面PQR，
则V=$\frac{1}{3}$S_△PQR•BD=$\frac{\sqrt{2}}{3}$．
则四面体BDPQ的体积为定值，故③正确；
若P，Q均在面对角线A₁C₁上，则四面体BDPQ在底面ABCD-A₁B₁C₁D₁上的投影恒为凸四边形，
则P、Q必在对角线B₁D₁的两侧，则PQ＞$\sqrt{2}$；
反之当PQ＞$\sqrt{2}$时，P、Q必在对角线B₁D₁的两侧，
四面体BDPQ在底面ABCD-A₁B₁C₁D₁上的投影恒为凸四边形，
故四面体BDPQ在底面ABCD-A₁B₁C₁D₁上的投影恒为凸四边形的充要条件是PQ＞$\sqrt{2}$，故④正确；
故正确结论的个数是3个，
故选：C

点评 本题以命题的真假判断为载体，考查了空间投影，三垂线定理，棱锥的体积，充要条件等知识点，综合性强，难度较大．