
【题目】已知函数f(x)=2sinωxcosωx+2 ![]() sin2ωx﹣
sin2ωx﹣ ![]() (ω>0)的最小正周期为π. (Ⅰ)求函数f(x)的单调增区间;
(ω>0)的最小正周期为π. (Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)将函数f(x)的图象向左平移 ![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象.若y=g(x)在[0,b](b>0)上至少含有10个零点,求b的最小值.
【答案】解:(Ⅰ)由题意,可得
f(x)= ![]() =
= ![]() .
.
∵函数的最小正周期为π,∴ ![]() =π,解之得ω=1.
=π,解之得ω=1.
由此可得函数的解析式为 ![]() .
.
令 ![]() ,解之得
,解之得 ![]()
∴函数f(x)的单调增区间是 ![]() .
.
(Ⅱ)将函数f(x)的图象向左平移 ![]() 个单位,再向上平移1个单位,可得函数y=f(x+
个单位,再向上平移1个单位,可得函数y=f(x+ ![]() )+1的图象,
)+1的图象,
∵ ![]()
∴g(x)= ![]() +1=2sin2x+1,可得y=g(x)的解析式为g(x)=2sin2x+1.
+1=2sin2x+1,可得y=g(x)的解析式为g(x)=2sin2x+1.
令g(x)=0,得sin2x=﹣ ![]() ,可得2x=
,可得2x= ![]() 或2x=
或2x= ![]()
解之得 ![]() 或
或 ![]() .
.
∴函数g(x)在每个周期上恰有两个零点,
若y=g(x)在[0,b]上至少含有10个零点,则b不小于第10个零点的横坐标即可,
即b的最小值为 ![]() .
.
【解析】(I)根据二倍角的三角函数公式与辅助角公式化简得 ![]() ,利用周期公式算出ω=1,得函数解析式为
,利用周期公式算出ω=1,得函数解析式为 ![]() .再由正弦函数单调区间的公式,解关于x的不等式即可得到函数f(x)的单调增区间;(II)根据函数图象平移的公式,得出函数g(x)的解析式为g(x)=2sin2x+1.由此解g(x)=0得sin2x=﹣
.再由正弦函数单调区间的公式,解关于x的不等式即可得到函数f(x)的单调增区间;(II)根据函数图象平移的公式,得出函数g(x)的解析式为g(x)=2sin2x+1.由此解g(x)=0得sin2x=﹣ ![]() ,利用正弦函数的图象解出
,利用正弦函数的图象解出 ![]() 或
或 ![]() ,可见g(x)在每个周期上恰有两个零点,若g(x)在[0,b]上至少含有10个零点,则b大于或等于g(x)在原点右侧的第10个零点,由此即可算出b的最小值.
,可见g(x)在每个周期上恰有两个零点,若g(x)在[0,b]上至少含有10个零点,则b大于或等于g(x)在原点右侧的第10个零点,由此即可算出b的最小值.
【考点精析】通过灵活运用两角和与差的正弦公式和正弦函数的单调性,掌握两角和与差的正弦公式:![]() ;正弦函数的单调性:在
;正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数即可以解答此题.
上是减函数即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C. (Ⅰ)证明:AC=AB1;
(Ⅱ)若AC⊥AB1 , ∠CBB1=60°,AB=BC,求二面角A﹣A1B1﹣C1的余弦值.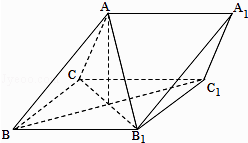
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若偶函数f(x)在区间[﹣1,0]上是减函数,α,β是锐角三角形的两个内角,且α≠β,则下列不等式中正确的是( )
A.f(cosα)>f(cosβ)
B.f(sinα)<f(cosβ)
C.f(cosα)<f(sinβ)
D.f(sinα)>f(sinβ)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),(x∈R,A>0,ω>0,|φ|< ![]() )的部分图象如图所示:
)的部分图象如图所示: 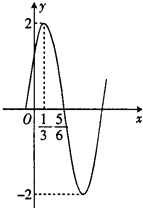
(1)试确定f(x)的解析式;
(2)若f( ![]() )=
)= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2﹣2x,g(x)=ax+2(a>0),对x1∈[﹣1,2],x0∈[﹣1,2],使g(x1)=f(x0),则a的取值范围是( )
A.![]()
B.![]()
C.[3,+∞)
D.(0,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=(﹣2m2+m+2)xm+1为偶函数.
(1)求f(x)的解析式;
(2)若函数y=f(x)﹣2(a﹣1)x+1在区间(2,3)上为单调函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商人如果将进货单价为 ![]() 元的商品按每件
元的商品按每件 ![]() 元出售,则每天可销售
元出售,则每天可销售 ![]() 件,现在他采用提高售价,减少进货量的办法增加利润.已知这种商品每件销售价提高
件,现在他采用提高售价,减少进货量的办法增加利润.已知这种商品每件销售价提高 ![]() 元,销售量就要减少
元,销售量就要减少 ![]() 件,如果使得每天所赚的利润最大,那么他应将每件的销售价定为( )
件,如果使得每天所赚的利润最大,那么他应将每件的销售价定为( )
A.![]() 元
元
B.![]() 元
元
C.![]() 元
元
D.![]() 元
元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com