
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:函数
满足:函数![]() 的图象关于直线
的图象关于直线![]() 对称,且当
对称,且当![]() 时
时![]() 是函数
是函数![]() 的导函数)成立.若
的导函数)成立.若![]() ,则
,则![]() 的大小关系是
的大小关系是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】![]() 函数
函数![]() 的图象关于直线
的图象关于直线![]() 对称,向左平移一个单位后得到函数
对称,向左平移一个单位后得到函数![]() 的图象,
的图象, ![]() 关于
关于![]() 轴对称,
轴对称, ![]() 为偶函数,
为偶函数, ![]() 函数
函数![]() 为奇函数,
为奇函数, ![]() ,
, ![]() 当
当![]() 时,
时, ![]() ,
, ![]() 函数
函数![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,函数
时,函数![]() 上单调递减,
上单调递减, ![]() ,
, ![]() ,
,
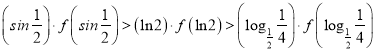 ,即
,即![]() ,故选A.
,故选A.
【方法点睛】本题主要考察抽象函数的单调性以及函数的求导法则,属于难题.求解这类问题一定要耐心读题、读懂题,通过对问题的条件和结论进行类比、联想、抽象、概括,准确构造出符合题意的函数是解题的关键;解这类不等式的关键点也是难点就是构造合适的函数,构造函数时往往从两方面着手:①根据导函数的“形状”变换不等式“形状”;②若是选择题,可根据选项的共性归纳构造恰当的函数.本题通过观察四个选项,联想到函数![]() ,再结合条件判断出其单调性,进而得出正确结论.
,再结合条件判断出其单调性,进而得出正确结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:![]() ),其频率分布直方图如下:
),其频率分布直方图如下:

(1)估计旧养殖法的箱产量低于50![]() 的概率并估计新养殖法的箱产量的平均值;
的概率并估计新养殖法的箱产量的平均值;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量 | 箱产量 | 合计 | |
旧养殖法 | |||
新养殖法 | |||
合计 |
附:![]() ,其中
,其中![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个命题,p:关于x的不等式ax>1(a>0,且a≠1)的解集是{x|x<0};q:函数y=lg(ax2﹣x+a)的定义域为R.如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() 万元,当年产量不足80千件时,
万元,当年产量不足80千件时, ![]() (万元);当年产量不少于80千件时,
(万元);当年产量不少于80千件时, ![]() (万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级的A,B,C三个班共有学生120人,为调查他们的体育锻炼情况,用分层抽样的方法从这三个班中分别抽取4,5,6名学生进行调查. (Ⅰ)求A,B,C三个班各有学生多少人;
(Ⅱ)记从C班抽取学生的编号依次为C1 , C2 , C3 , C4 , C5 , C6 , 现从这6名学生中随机抽取2名做进一步的数据分析.
(i)列出所有可能抽取的结果;
(ii)设A为事件“编号为C1和C2的2名学生中恰有一人被抽到”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公比为正数的等比数列{an}中, ![]() ,
, ![]() ,数列{bn}(bn>0)的前n项和为Sn满足
,数列{bn}(bn>0)的前n项和为Sn满足 ![]() (n≥2),且S10=100.
(n≥2),且S10=100.
( I)求数列{an}和数列{bn}的通项公式;
( II)求数列{anbn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
在平面直角坐标系xoy中,曲线![]() ,直线
,直线![]() 过点
过点![]() 与曲线
与曲线![]() 交于
交于![]() 二点,
二点, ![]() 为
为![]() 中点.以坐标原点O为极点,x轴正半轴为极轴,以平面直角坐标系xoy的单位1为基本单位建立极坐标系.
中点.以坐标原点O为极点,x轴正半轴为极轴,以平面直角坐标系xoy的单位1为基本单位建立极坐标系.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2) ![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,| ![]() |=|
|=| ![]() |=|
|=| ![]() |=1,
|=1, ![]() ,A(1,1),则
,A(1,1),则 ![]() 的取值范围( )
的取值范围( )
A.[﹣1﹣ ![]() ,
, ![]() ﹣1]
﹣1]
B.[﹣ ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() +
+ ![]() ]?
]?
C.[ ![]() ﹣
﹣ ![]() ,
, ![]() +
+ ![]() ]
]
D.[1﹣ ![]() ,1+
,1+ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每台新机随机购买第一盒墨150元,优惠0元;再每多买一盒墨都要在原优惠基础上多优惠一元,即第一盒墨没有优惠,第二盒墨优惠一元,第三盒墨优惠2元,……,依此类推,每台新机最多可随新机购买25盒墨.平时购买墨盒按零售每盒200元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如下表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
以这十台打印机消耗墨盒数的频率代替一台打印机消耗墨盒数发生的概率,记ξ表示两台打印机5年消耗的墨盒数.
(1)求ξ的分布列;
(2)若在购买两台新机时,每台机随机购买23盒墨,求这两台打印机正常使用五年在消耗墨盒上所需费用的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com