
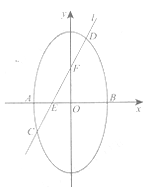
【题目】椭圆![]() 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线![]() 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设直线AD,CB的斜率分别为![]() ,若
,若![]() ,求k的值.
,求k的值.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆的焦点,直线
是椭圆的焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,求
的面积最大时,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是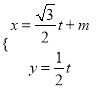 (
(![]() 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程式为
的极坐标方程式为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心为坐标原点,其离心率为
的中心为坐标原点,其离心率为![]() ,椭圆
,椭圆![]() 的一个焦点和抛物线
的一个焦点和抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆![]() 的方程
的方程![]()
(2)过点![]() 的动直线
的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,试问:在平面上是否存在一个定点
两点,试问:在平面上是否存在一个定点![]() ,使得无论
,使得无论![]() 如何转动,以
如何转动,以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,若存在,说出点
,若存在,说出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位数学老师组队参加某电视台闯关节目,共3关,甲作为嘉宾参与答题,若甲回答错误,乙作为亲友团在整个通关过程中至多只能为甲提供一次帮助机会,若乙回答正确,则甲继续闯关,若某一关通不过,则收获前面所有累积奖金.约定每关通过得到奖金2000元,设甲每关通过的概率为![]() ,乙每关通过的概率为
,乙每关通过的概率为![]() ,且各关是否通过及甲、乙回答正确与否均相互独立.
,且各关是否通过及甲、乙回答正确与否均相互独立.
(1)求甲、乙获得2000元奖金的概率;
(2)设![]() 表示甲、乙两人获得的奖金数,求随机变量
表示甲、乙两人获得的奖金数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|ax-x2|+2b(a,b∈R).
(1)当b=0时,若不等式f(x)≤2x在x∈[0,2]上恒成立,求实数a的取值范围;
(2)已知a为常数,且函数f(x)在区间[0,2]上存在零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中![]() 所表示的数分别是多少?
所表示的数分别是多少?
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?由直方图确定此组数据中位数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com