
【题目】设椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]()
![]() ,点D在椭圆C上,
,点D在椭圆C上,![]() 的周长为
的周长为![]() .
.
(1)求椭圆C的标准方程;
(2)过圆![]() 上任意一点P作圆E的切线l,若l与椭圆C交于A,B两点,O为坐标原点,求证:
上任意一点P作圆E的切线l,若l与椭圆C交于A,B两点,O为坐标原点,求证:![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,定义
,定义![]() 为
为![]() 的“优值”.现已知某数列的“优值”为
的“优值”.现已知某数列的“优值”为 ![]() ,记数列
,记数列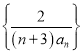 的前
的前![]() 项和为
项和为![]() ,若对一切的
,若对一切的![]() ,都有
,都有![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为___________.
的取值范围为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
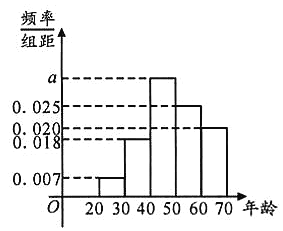
、![]() 分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
分成了五组,其频率分布直方图如下图所示,参保年龄与每人每年应交纳的保费如下表所示.
年龄(单位:岁) |
|
|
|
|
|
保费(单位:元) |
|
|
|
|
|
(1)求频率分布直方图中实数![]() 的值,并求出该样本年龄的中位数;
的值,并求出该样本年龄的中位数;
(2)现分别在年龄段![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中各选出
中各选出![]() 人共
人共![]() 人进行回访.若从这
人进行回访.若从这![]() 人中随机选出
人中随机选出![]() 人,求这
人,求这![]() 人所交保费之和大于
人所交保费之和大于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 在点
在点![]() 处的切线斜率为0.
处的切线斜率为0.
(1)试用含有![]() 的式子表示
的式子表示![]() ,并讨论
,并讨论![]() 的单调性;
的单调性;
(2)对于函数![]() 图象上的不同两点
图象上的不同两点![]() ,
,![]() ,如果在函数
,如果在函数![]() 图象上存在点
图象上存在点![]() ,使得在点
,使得在点![]() 处的切线
处的切线![]() ,则称
,则称![]() 存在“跟随切线”.特别地,当
存在“跟随切线”.特别地,当![]() 时,又称
时,又称![]() 存在“中值跟随切线”.试问:函数
存在“中值跟随切线”.试问:函数![]() 上是否存在两点
上是否存在两点![]() 使得它存在“中值跟随切线”,若存在,求出
使得它存在“中值跟随切线”,若存在,求出![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
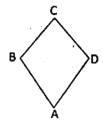
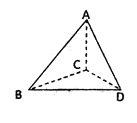
【题目】等腰直角三角形BCD与等边三角形ABD中,![]() ,
,![]() ,现将
,现将![]() 沿BD折起,则当直线AD与平面BCD所成角为
沿BD折起,则当直线AD与平面BCD所成角为![]() 时,直线AC与平面ABD所成角的正弦值为( )
时,直线AC与平面ABD所成角的正弦值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若对![]() 时,不等式
时,不等式![]() 恒成立,求实数a的取值范围(e为自然对数的底数);
恒成立,求实数a的取值范围(e为自然对数的底数);
(2)当![]() 时,求函数
时,求函数![]() 的极大值;
的极大值;
(3)求证:当![]() 时,曲线
时,曲线![]() 与直线
与直线![]() 有且仅有一个公共点.
有且仅有一个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
: ![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得当
,使得当![]() 变动时,总有直线
变动时,总有直线![]() 的斜率之和为0?若存在,求出
的斜率之和为0?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com