Question

【题目】已知圆M过两点A（1，﹣1），B（﹣1，1），且圆心M在直线x+y﹣2=0上．

（1）求圆M的方程．

（2）设P是直线3x+4y+8=0上的动点，PC、PD是圆M的两条切线，C、D为切点，求四边形PCMD面积的最小值．

Answer 1

【答案】（1）（x﹣1）2+（y﹣1）2=4．（2）2．

【解析】

试题分析：（1）设圆心M（a，b），依题意，可求得AB的垂直平分线l的方程，利用方程组可求得直线l与直线x+y﹣2=0的交点，即圆心M（a，b），再求得r=|MA|=2，即可求得

圆M的方程；

（2）作出图形，易得SPCMD=|MC||PC|=2=2，利用点到直线间的距离公式可求得|PM|min=d=3，从而可得（SPCMD）min=2．

解：（1）设圆心M（a，b），则a+b﹣2=0①，

又A（1，﹣1），B（﹣1，1），

∴kAB==﹣1，

∴AB的垂直平分线l的斜率k=1，又AB的中点为O（0，0），

∴l的方程为y=x，而直线l与直线x+y﹣2=0的交点就是圆心M（a，b），

由解得：，又r=|MA|=2，

∴圆M的方程为（x﹣1）2+（y﹣1）2=4．

（2）如图：

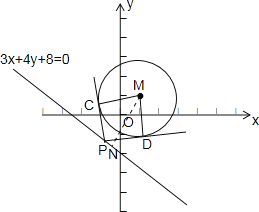
SPCMD=|MC||PC|=2=2，

又点M（1，1）到3x+4y+8=0的距离d=|MN|==3，

所以|PM|min=d=3，

所以（SPCMD）min=2=2．